| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- 리액트
- 프로그래머스
- 프로그래머스코테
- JS프로그래머스
- 코딩테스트
- 백준
- 백준구현문제
- 코테
- js코테
- 안드로이드 스튜디오
- 알고리즘
- css기초
- 리액트커뮤니티
- HTML5
- 익스프레스
- 다이나믹프로그래밍
- 프로그래머스JS
- 자바스크립트
- 백준알고리즘
- HTML
- 리액트댓글기능
- dp알고리즘
- CSS
- 백준js
- 백준nodejs
- 백준골드
- 몽고DB
- 포이마웹
- 백준구현
- JS
- Today
- Total
개발새발 로그
플로이드 와샬(Floyd warshall)알고리즘 본문
다익스트라 알고리즘은 [하나의 정점에서 출발 했을 때 다른 모든 정점으로의 최단 경로를 구하는 알고리즘]입니다.
만약 [모든 정점에서 모든 정점으로의 최단 경로]를 구하고 싶다면 플로이드 와샬 알고리즘을 사용해야합니다.
다익스트라 알고리즘은 가장 적은 비용을 하나씩 선택해야 했다면
플로이드 와샬 알고리즘은 기본적으로 거쳐가는 정점을 기준으로 알고리즘을 수행한다느 점입니다.
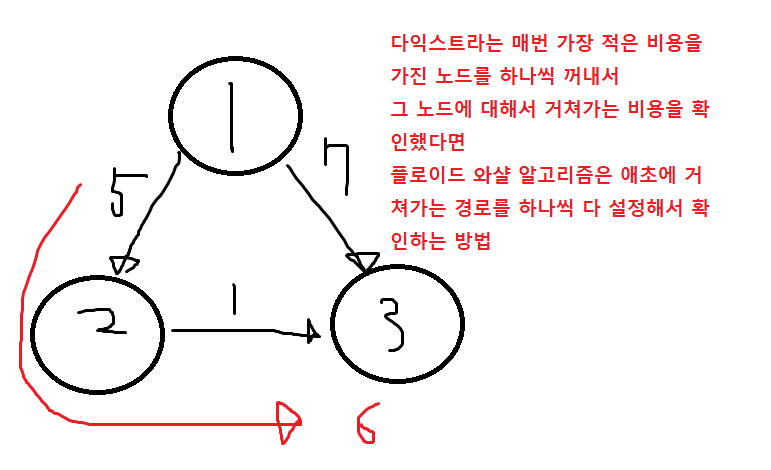
다음과 같은 그래프가 있다고 가정해보자

이때 각각의 정점이 다른 정점으로 가는 최소비용을 이차원 배열의 형태로 출력하면 다음과 같다.
| 0 [1->1] | 2 [1->2] | 4 | Infinity | Infinity |
| 3 [2->1] | 0 [2->2] | 5 | 2 | Infinity |
| Infinity | Infinity | 0 | 7 | 4 |
| Infinity | Infinity | Infinity | 0 | 3 |
| Infinity | Infinity | Infinity | 6 | 0 |
다익스트라에서는 오직 1차원배열을 사용해서 특정한 노드 한개(ex. 1에서부터 모든 정점)에서 갈 수 있는 최단경로 값을 넣어줬었다.
하지만 플로이드 와샬은 2차원배열을 사용한다는 것이다.
모든정점에서 모든정점으로 가는 최단경로값을 넣는다.
이러한 2차원 배열을 반복적으로 갱신해서 최종적으로 모든 최소비용을 구해야 한다.
바로 그래서 반복의 기준이 거쳐가는 정점이라고 한 것이다,
1. 노드 1을 거쳐가는 경우 (1과 연관되지않은 부분이 갱신가능한 부분 즉 1이 포함되는경우제외)

| 0 [1->1] | 2 [1->2] | 4 | Infinity | Infinity |
| 3 [2->1] | 0 [2->2] | 갱신이 가능한 부분 [2->3] |
갱신이 가능한 부분 | 갱신이 가능한 부분 |
| Infinity | 갱신이 가능한 부분 | 0 | 갱신이 가능한 부분 | 갱신이 가능한 부분 |
| Infinity | 갱신이 가능한 부분 | 갱신이 가능한 부분 | 0 | 갱신이 가능한 부분 |
| Infinity | 갱신이 가능한 부분 | 갱신이 가능한 부분 | 갱신이 가능한 부분 | 0 |
이제 여기서 갱신을해줘야한다.
예를 들어보자
2에서3으로 가는부분 [2->3] 은 5다.
이것을 [2->1] + [1->3] 과 비교해준다. [1을 거쳐간다는 특징] -> 이게 어떤걸 거쳐가는지가 기준이 되는 것이다.
-즉 2에서 1로 갔다가 1에서 3으로 가는 것이다.
5 < 3 + 4 가 된다. (5가 작음) 갱신할 필요가 없음
X에서 Y로 가는 최소 비용 VS X에서 노드 1로 가는 비용 + 노드 1에서 Y로 가는 비용
이런식으로 모두 계산하면된다.
| 0 [1->1] | 2 [1->2] | 4 | Infinity | Infinity |
| 3 [2->1] | 0 [2->2] | 5 | 2 | Infinity |
| Infinity | Infinity | 0 | 7 | 4 |
| Infinity | Infinity | Infinity | 0 | 3 |
| Infinity | Infinity | Infinity | 6 | 0 |
1. 노드 2를 거쳐가는 경우 (2와 연관되지않은 부분이 갱신가능한 부분, 즉 2가 포함되는경우 제외)

| 0 [1->1] | 2 [1->2] | 갱신이 가능한 부분 | 갱신이 가능한 부분 | 갱신이 가능한 부분 |
| 3 [2->1] | 0 [2->2] | 5 | 2 | Infinity |
| 갱신이 가능한 부분 | Infinity | 0 | 갱신이 가능한 부분 | 갱신이 가능한 부분 |
| 갱신이 가능한 부분 | Infinity | 갱신이 가능한 부분 | 0 | 3 |
| 갱신이 가능한 부분 | Infinity | 갱신이 가능한 부분 | 6 | 0 |
아래와 같이 1->3을 가는 경우를 1->2->3의 경우와 비교한다.
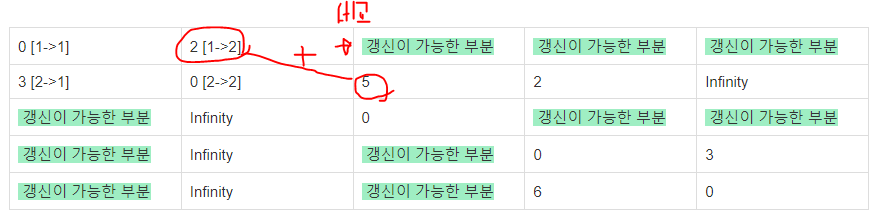
이러한 방식을 모든 노드에서 수행한다.
그럼 아래와 같은 배열이 나오게 된다.-현재 그래프에서 3->1 로 가는 간선이 없어서 infinity가나온다. 다른 infinity도 마찬가지라서 infinity가 포함된다. -> 그래프 잘만들면됨
| 0 [1->1] | 2 [1->2] | 4 | 4 | 7 |
| 3 [2->1] | 0 [2->2] | 5 | 2 | 5 |
| Infinity | Infinity | 0 | 7 | 4 |
| Infinity | Infinity | Infinity | 0 | 3 |
| Infinity | Infinity | Infinity | 6 | 0 |
코드로 바꿔보자
const INF= Infinity;
const a=[
[0,2,4,INF,INF],
[3,0,5,2,INF],
[INF,INF,0,7,4],
[INF,INF,INF,0,3],
[INF,INF,INF,6,0]
]
const number = a.length;
function floyd(){
//결과 그래프를 초기화
let d = Array.from({length:number},()=>Array(number).fill());
for(var i=0;i<number;i++){
for(var j=0;j<number;j++){
d[i][j]=a[i][j];
}
}
//k는 거쳐가는 노드
for(var k=0; k<number;k++){
//i= 출발 노드
for(var i=0;i<number;i++){
//j = 도착 노드
for(var j=0;j<number;j++){
//1을 거쳐가는 반복문에서 2->3값을 갱신한다고 할 때
//예를 들어 2->3값과 2->1->3 값을 비교한다
if(d[i][k] + d[k][j] < d[i][j]) {
d[i][j] = d[i][k] + d[k][j];
}
}
}
}
console.log(d);
}
floyd();
출처
https://blog.naver.com/ndb796/221234427842
24. 플로이드 와샬(Floyd Warshall) 알고리즘
지난 시간에는 다익스트라(Dijkstra) 알고리즘에 대해 학습했습니다. 다익스트라 알고리즘은 하나...
blog.naver.com
예제
문제 설명
n명의 권투선수가 권투 대회에 참여했고 각각 1번부터 n번까지 번호를 받았습니다. 권투 경기는 1대1 방식으로 진행이 되고, 만약 A 선수가 B 선수보다 실력이 좋다면 A 선수는 B 선수를 항상 이깁니다. 심판은 주어진 경기 결과를 가지고 선수들의 순위를 매기려 합니다. 하지만 몇몇 경기 결과를 분실하여 정확하게 순위를 매길 수 없습니다.
선수의 수 n, 경기 결과를 담은 2차원 배열 results가 매개변수로 주어질 때 정확하게 순위를 매길 수 있는 선수의 수를 return 하도록 solution 함수를 작성해주세요.
제한 사항
- 선수의 수는 1명 이상 100명 이하입니다.
- 경기 결과는 1개 이상 4,500개 이하입니다.
- results 배열 각 행 [A, B]는 A 선수가 B 선수를 이겼다는 의미입니다.
- 모든 경기 결과에는 모순이 없습니다.
입출력 예
nresultsreturn
5 [[4, 3], [4, 2], [3, 2], [1, 2], [2, 5]] 2
입출력 예 설명
2번 선수는 [1, 3, 4] 선수에게 패배했고 5번 선수에게 승리했기 때문에 4위입니다.
5번 선수는 4위인 2번 선수에게 패배했기 때문에 5위입니다.
1. 이 문제의 첫번째 키 포인트는 내 순위를 확실히 알아야한다는 점입니다.
2. 그 말은 즉, 행을 기준 한 행에 1또는 -1값이 n-1개수만큼있을 때, 내 순위를 확실히 알 수 있습니다.
->즉 false의 갯수가 하나인 배열은 순위가 구해진다.
3.두 번째로 "A를 이긴 사람들은 A에게 패배한 사람들을 무조건 이긴다." 를 기억해주시면 되는데,
4. 위의 예제에서는 5번 선수는 1,3,4에게 무조건 패배한다가 성립되겠죠? 반대로 1,3,4선수는 5번선수를 무조건 이기는게 성립이 될 것입니다.
function solution(results) {
let answer = 0;
let n=results.length
const graph = Array.from({length:n+1},()=>Array(n+1).fill(false)}
//각 정점 사이, 즉 선수들 사이에 경기가 이루어졌는지 여부와 만약 경기가 이루어진 경우라면
//누가 이겼는지에 대한 정보를 이차원 배열에 넣어줘야 한다.
//A 선수와 B 선수 사이의 경기 여부 및 결과 = graph[A][B] 이런식으로 값을 넣어 준다.
results.forEach((v)=>{
const [A,B] = v;
graph[A][B] = 1;
graph[B][A] = -1;
graph[A][A] = 0;
graph[B][B] = 0;
});
//A 선수가 B 선수를 이긴 경우에는 1,
//A 선수가 B 선수에게 진 경우에는 -1,
//둘 사이의 경기가 없었다면 false 값만 남아있게 될 것이다.
//자기 자신에서 자기 자신에게 가는 경우는 0으로 값을 입력)
//pass는 거쳐가는 선수 -> 1번선수부터
for(let pass=0; pass<n+1; pass++){
//start는 거쳐가는 선수와 대결한 선수
for(let start=0; start<n+1; start++){
//near은 거쳐가는 선수와 대결한 선수
for(let near=0; near<n+1; near++){
// 이기는 경우( A와 1번선수 == 승리 && 1번선수와 B선수== 승리) A선수는 B선수 이김
//1번선수가 A한테는 지지만 B는 이김
if(graph[start][pass] === 1 && graph[pass][near] === 1) graph[start][near] = 1;
// 지는 경우(A와 1번선수==패배 && 1번선수와 B선수 == 패배) A선수는 B선수한테 패배함
//1번선수가 A를 이기고, 1번선수가 B한테 지면 A는 B한테 무조건 진다.
if(graph[start][pass] === -1 && graph[pass][near] === -1) graph[start][near] = -1;
}
}
}
//그래프를 순회하면서 false가 하나인것을 찾는다. 즉 4개의 경기를 진행했으므로 순위를 알 수 있다.
graph.forEach((line)=>{
if(line.filter((v)=> v === false).length === 1){
answer++;
}
})
return answer;
}
console.log(solution([[4, 3], [4, 2], [3, 2], [1, 2], [2, 5]]))
reuslt배열 값

[AL] 플로이드 와샬 알고리즘 (Floyd-Warshall) - JavaScript
하나의 정점을 출발점으로 지정하여 모든 정점까지의 최단 거리를 구하는 다익스트라 알고리즘,모든 정점들을 출발점으로 지정하여 모든 정점까지의 최단 거리를 구하는 플로이드 와샬 알고리
velog.io
https://minnnne.tistory.com/91
프로그래머스 - 순위(Level 3)/Wanna Be 컴잘알
문제 출처 - https://programmers.co.kr/learn/courses/30/lessons/49191#qna 프로그래머스 코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합
minnnne.tistory.com
'알고리즘' 카테고리의 다른 글
| 에라토스테네스의 체 (0) | 2023.06.04 |
|---|---|
| 위상 정렬 (0) | 2023.06.03 |
| 다익스트라 알고리즘 (2) | 2023.06.02 |
| 다이나믹 프로그래밍 (Dynamic Programming) - 타일링문제 2 (0) | 2023.06.01 |
| 다이나믹 프로그래밍(Dynamic Programming) - 타일링 문제 (0) | 2023.05.31 |