| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- HTML
- 프로그래머스코테
- CSS
- 리액트
- 익스프레스
- dp알고리즘
- 백준알고리즘
- 백준구현문제
- 백준구현
- JS
- 백준js
- 알고리즘
- 프로그래머스
- 몽고DB
- 백준골드
- 코딩테스트
- js코테
- 백준
- 안드로이드 스튜디오
- css기초
- 자바스크립트
- 다이나믹프로그래밍
- HTML5
- 프로그래머스JS
- 코테
- 백준nodejs
- 리액트댓글기능
- JS프로그래머스
- 포이마웹
- 리액트커뮤니티
- Today
- Total
개발새발 로그
그래프이론(서로소집합) 본문
- 서로소 집합이란 공통 원소가 없는 두 집합을 의미한다.
- 서로소 집합 자료구조란 서로소 부분 집합들로 나누어진 원소들의 데이터를 처리하기 위한 자료구조
- 서로소 집합 자료구조는 합집합(union)과 찾기(find) 연산으로 구성
쉽게보면 현재 연결되지않은 노드들이 있는 것이다. 그래서 공통된원소가 없어 서로 합쳐야하는 것이다.

그림을 보면 현재 부모값과 노드값이 똑같다.
이제 이걸 {1 , 2} 두 원소를 합칠 것이다.
합치게되면 1 의 parent값 1과 2의 parent값 2를 같게해서 연결되게 할것이다.
-> 부모 값이 같음으로써 서로 연결되어 합쳐 졌다는 의미가 된다.
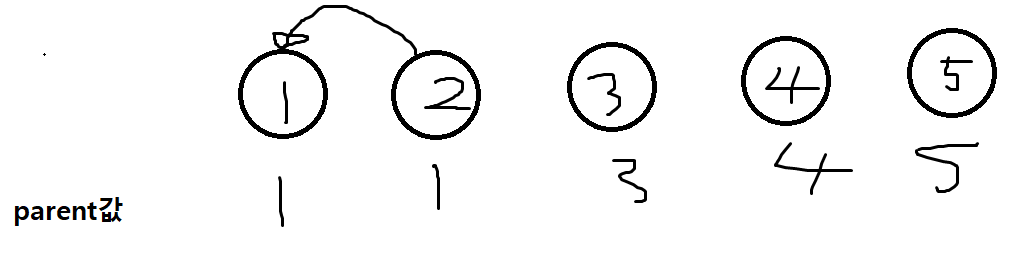
즉 위와같은 경우가 되는것이다.
2의 부모값을 1로 바꿔준다. -> 바꿔줄 때 부모 값이 작은 쪽이 부모가 되도록 해야한다.
이제 합치고 이를 확인하기 위해 3개의 함수가 필요하다.
두 개의 원소를 합치는 union이라는 함수를 만들고,
1의 부모값을 가져오는 getParent함수를 만들고,
1의 부모값과 2의 부모값이 같은지(합쳐졌는지) 확인하는 findParent함수를 만들어야한다.
getParent함수 - 현재 노드의 부모값을 가져오는 함수
const getParent = (parent, x) => {
if (parent[x] === x) return parent[x];
return (parent[x] = getParent(parent, parent[x]));
};현재 parent값을 가져오는 함수이다.
원리가 어떻게 되냐면

이 그림을 보고 해보자
내가 2의 부모값을 찾을건데 2의 부모값이 2면 같으니까 2의 부모값은 2가 맞다. -> 그래서 2의 부모값 2를 반환한다.
---
근데 만약 아래와 같은 상황이면 어떻게 되는지 보자

2와 1이 union을 통해 합쳐진 상태다.
그럼 2의 부모값은 1이다.
if (parent[x] === x) 이 조건에 부합하지 않는다.
그럼 parent[x] 즉 2의 부모 값은 다시 getParent함수를 재귀적으로 호출하게 된다.
부모 배열과 2의 부모값을 1을 넘겨준다.
그럼 그 다음 getParent함수는 1의 부모값을 찾게된다.
1의 부모값은 1로 같다. -> 그럼 1을 반환하게 된다.
그래서 2의 getParent함수를 통해 얻은 부모값은 1이 되는 것이다.
Union함수 - 두 노드의 값을 합치는 함수
const unionParent = (parent, a, b) => {
a = getParent(parent, a);
b = getParent(parent, b);
if (a < b) parent[b] = a;
else parent[a] = b;
};이제 합치는 함수다.
일단 현재 아래의 그림같이 초기화가 되어있다고 가정하자.

합치고싶은 {1 , 2} 노드가 있다면 그걸 a와 b 로 준다.
getParent함수를 통해서 현재 1과 2의 부모값을 가져온다. -> parent[1] = 1, parent[2] =2
가져온 값을 비교한다. 1 < 2
그럼 1이 작은 값인데 이 때
if (a < b) parent[b] = a;이걸 통해 parent[2]의 부모값을 1로 바꾼다.
여기서중요한 점은 위 getParent함수로 parent[2] =2 로 인해 b값은 초기화 되어있다.
->이게 만약에 parent[2] = 1 이면 b는 1이 된다.
->그럼 if(a<b) parent[b] = a에서 parent[1]= a 가 된다.
->즉 만약에 2의 부모값이 자신과 다른 상황이라면 2의 부모값의 부모값을 바꾸는 것이다.
예를 들어보자.

{1, 2} 와 {3, 5}는 서로소집합이다.
만약 2와 5를 union을 한다고 생각하자.
그럼 union함수를 통해서
2의 부모값 a=1
5의 부모값 b=3
1 < 3 이므로 parent[b] = a 가 된다. -> 즉 parent[3]= 1 이된다.
5의 부모값이 바뀌는 게 아닌 3의 부모값이 1로 바뀌어 버리는 것이다.

이를 통해서 서로소집합이었던 두 집합은 위와 같이 연결되어졌다.
중요한건
만약에 5와 1이 연결되어있는지
혹은 2와 5가 연결되어있는지
혹은 3과 1이 연결되어있는지 확인하는 findParent에서는 모두 연결되어있다라고 나온다.
findParent함수 - 두 노드의 부모 값이 같은지(즉 연결되어있는지) 확인하는 함수
const findParent = (parent, a, b) => {
a = getParent(parent, a);
b = getParent(parent, b);
if(a==b) return 1;
else return 0;
};두 노드 a와 b의 부모 값을가져와서 같은지 확인한다.
위에서 아까 했던 그림을 가져와보자.

이 상태에서 2 와 5가 연결되어있는지 확인해보자
2의 부모값을 가져오면 1이다.
5의 부모값을 가져오면 3이여야하는데 3이아닌 1이다.
-> 이게 무슨소리냐면 getParent는 재귀적으로 노드값과 부모값이 같을 때 반환된다.
->즉, 5의 부모값 3은 parent[3]의 값과 다르므로 다시 getParent함수로 3의 부모값 1을 탐색한다.
->그럼 결국 1이라는 값이 나온다
그럼 a의 값은 1이고
b의값도 1이므로
두 노드는 연결되어있다라고 확인된다.
전체 소스 코드
const findParent = (parent, a, b) => {
a = getParent(parent, a);
b = getParent(parent, b);
if(a==b) return 1;
else return 0;
};
const unionParent = (parent, a, b) => {
a = getParent(parent, a);
b = getParent(parent, b);
if (a < b) parent[b] = a;
else parent[a] = b;
};
const getParent = (parent, x) => {
if (parent[x] === x) return parent[x];
return (parent[x] = getParent(parent, parent[x]));
};
//parent배열을 인덱스와 값을 동일하게 초기화(자기자신이 부모값이됨-연결되오있지 않음)
for(var i=1;i<10;i++){
parent[i]=i;
}
unionParent(parent,1,2);
unionParent(parent,2,3);
unionParent(parent,3,4);
findParent(parent,1,4);
console.log("1과 4는 서로 연결되어있습니까?"+findParent(parent,1,4) ? "yes" : "No");
https://chanhuiseok.github.io/posts/baek-25/
[백준] 10775번 - 공항 (서로소 집합 알고리즘 활용)
컴퓨터/IT/알고리즘 정리 블로그
chanhuiseok.github.io
서로소집합 예제를 보면서 이해해보자
이 알고리즘을 통해서 나중에 크루스칼 알고리즘에 이용된다.
다음 포스트에서 설명해야겠다.
출처
https://blog.naver.com/ndb796/221230967614
'알고리즘' 카테고리의 다른 글
| 다이나믹 프로그래밍(Dynamic Programming) - 타일링 문제 (1) | 2023.05.31 |
|---|---|
| 다이나믹 프로그래밍(Dynamic Programming) - 메모제이션 (1) | 2023.05.31 |
| 그래프 이론 (이진트리의 구현과 순회방식) (1) | 2023.05.31 |
| 그래프 이론(크루스칼 알고리즘) (0) | 2023.05.31 |
| 누적합(prefix sum) (0) | 2023.05.31 |