| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 리액트댓글기능
- 자바스크립트
- 프로그래머스JS
- 백준골드
- 백준구현
- 몽고DB
- 프로그래머스코테
- 알고리즘
- js코테
- 리액트커뮤니티
- 포이마웹
- dp알고리즘
- 백준구현문제
- 백준
- 다이나믹프로그래밍
- JS
- 백준js
- css기초
- JS프로그래머스
- 코딩테스트
- 코테
- 프로그래머스
- CSS
- 리액트
- 백준nodejs
- 백준알고리즘
- HTML
- 익스프레스
- HTML5
- 안드로이드 스튜디오
- Today
- Total
개발새발 로그
[2023-09-26] 자료구조 & 알고리즘 - 힙 본문

우선순위 큐
- FIFO인 큐와 달리 우선순위가 높은 요소가 먼저 나가는 큐
- 이때 우선순위 큐는 자료구조가 아닌 개념이다.
우선순위 큐를 구현하는 방법은 다양하게 존재한다.
그 중 힙은 우선순위 큐를 구현하기에 가장 적합한 방법이다.
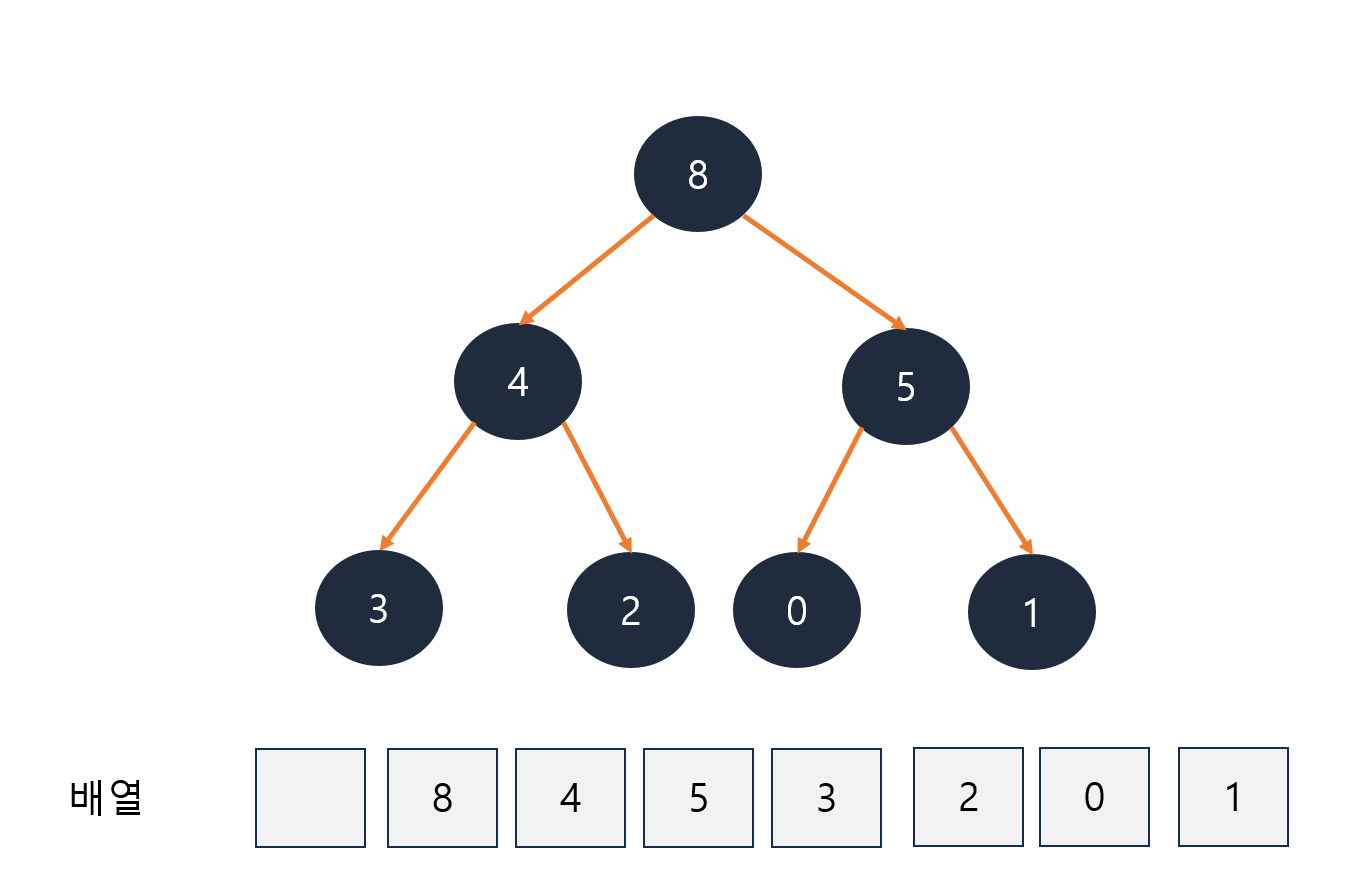
힙
- 이진 트리 형태를 가지며 우선순위가 높은 요소가 먼저 나가기 위해 요소가 삽입, 삭제 될 때 정렬되는 특징이 있다.
우선순위 큐와 힙은 다른 것이다!
-만약 배열을 매번 우선순위에 따라 정렬하면 그것도 우선순위 큐가 될 수 있다. 단지 힙보다 효율이 떨어질 뿐이다.
힙의 특징
- 우선순위가 높은 요소가 먼저나가는 특징을 가진다.
- 루트가 가장 큰 값이 되는 최대 힙과 루트가 가장 작은 값이 되는 최소 힙이 있다.
- 아쉽게도 자바스크립트에서는 직접 구현해서 사용해야 한다.
힙의 요소 추가
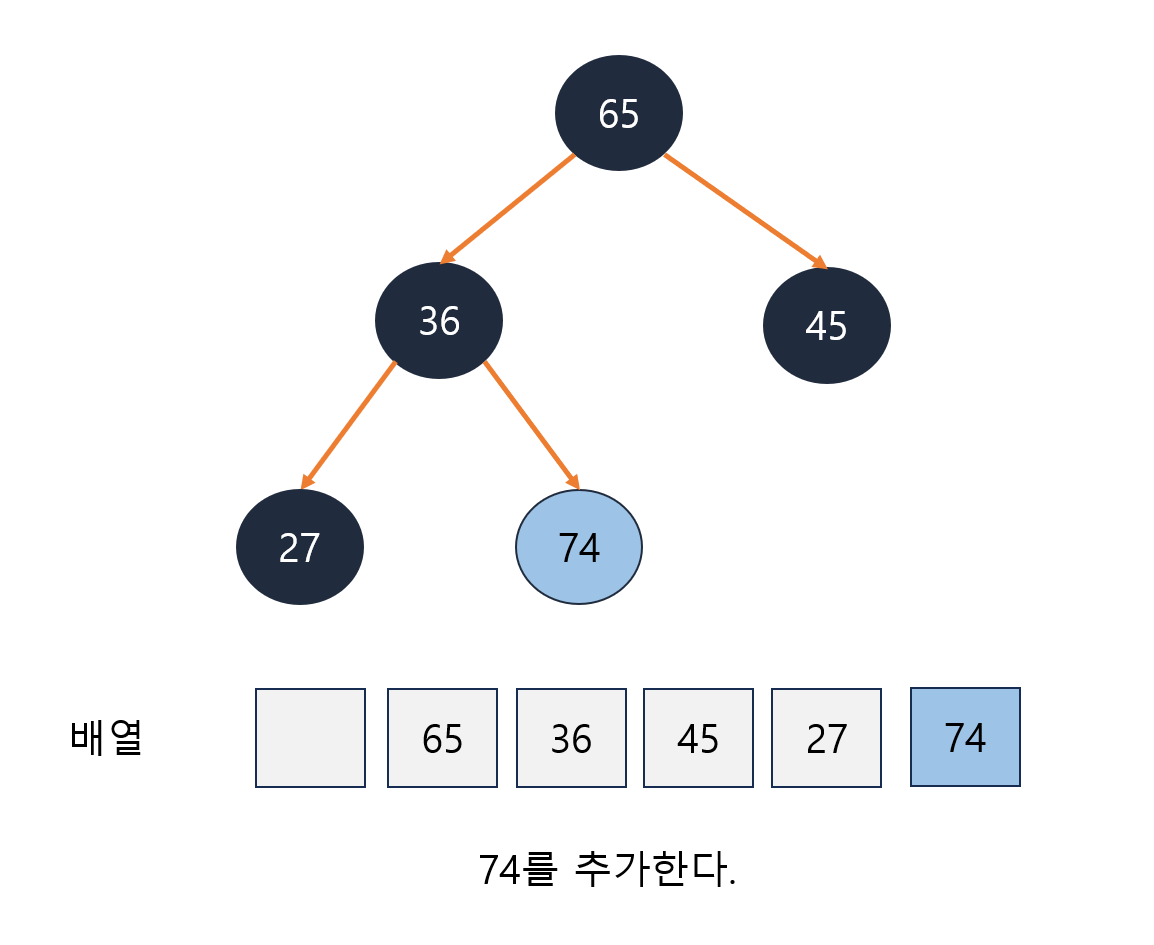
- 요소가 추가될 때는 트리의 가장 마지막 정점에 위치한다. - 힙은 항상 완전 이진트리
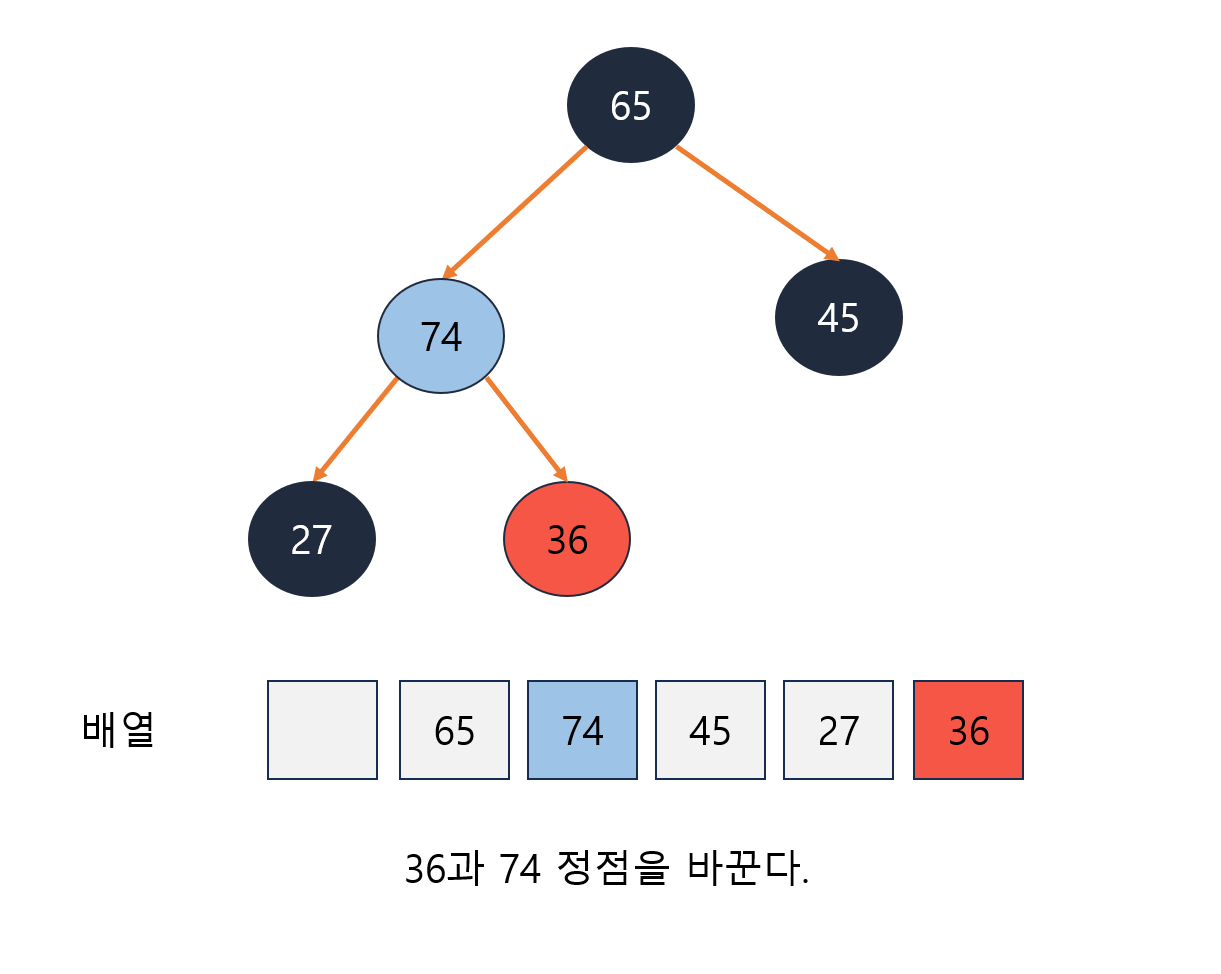
- 추가 후 부모 정점보다 우선순위가 높다면 부모 정점과 순서를 바꾼다.
- 이 과정을 반복하면 가장 우선순위가 높은 정점이 루트가 된다.
- 완전 이진 트리의 높이는 Log N이기에 힙의 요소 추가 알고리즘은 O(log N) 시간 복잡도를 가진다.
힙의 추가 동작 과정
1.
2.

3.
4.

5.

7.

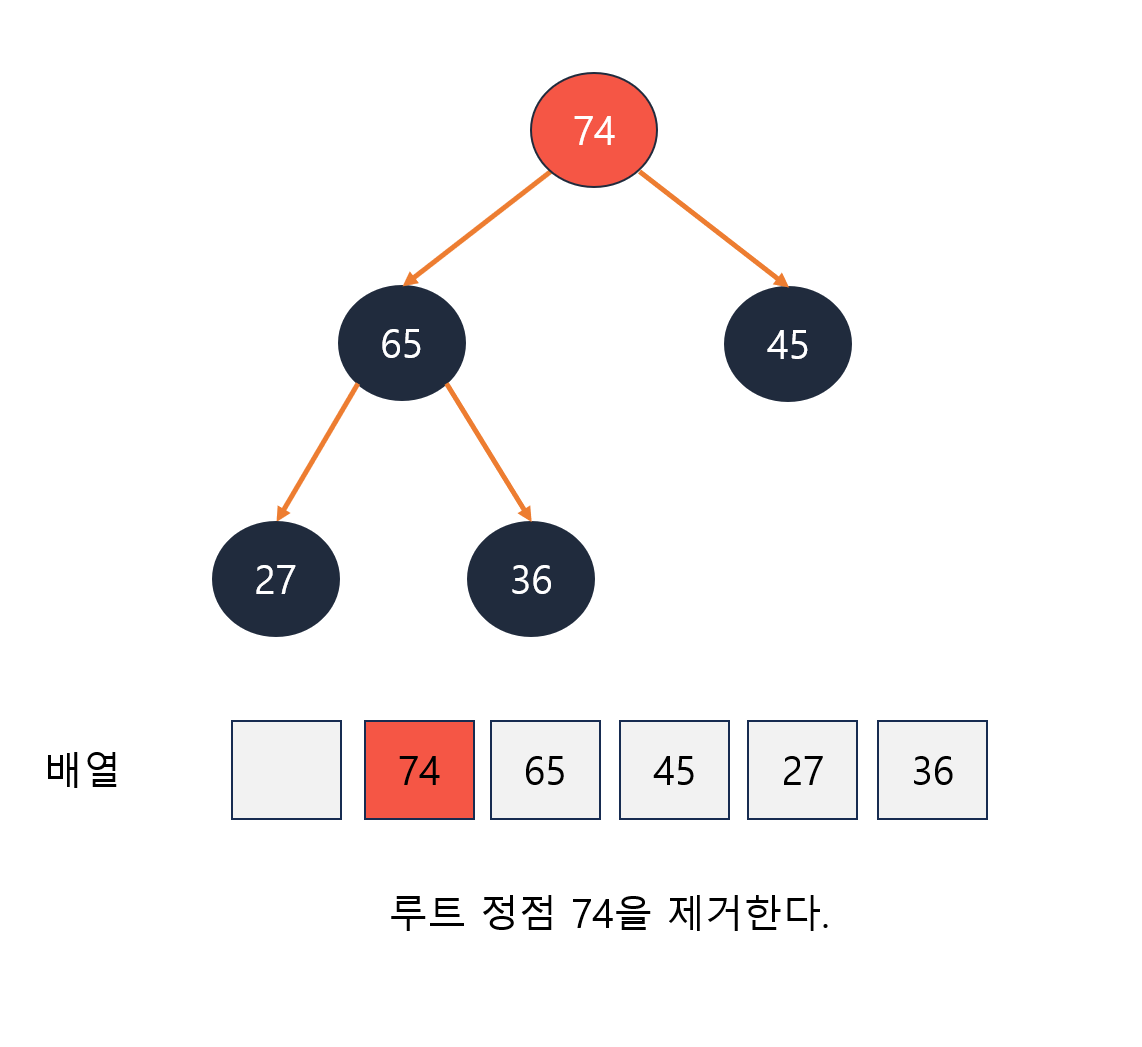
힙의 요소 제거
-요소 제거는 루트 정점만 가능하다
- 루트 정점이 제거된 후 가장 마지막 정점이 루트에 위치한다.
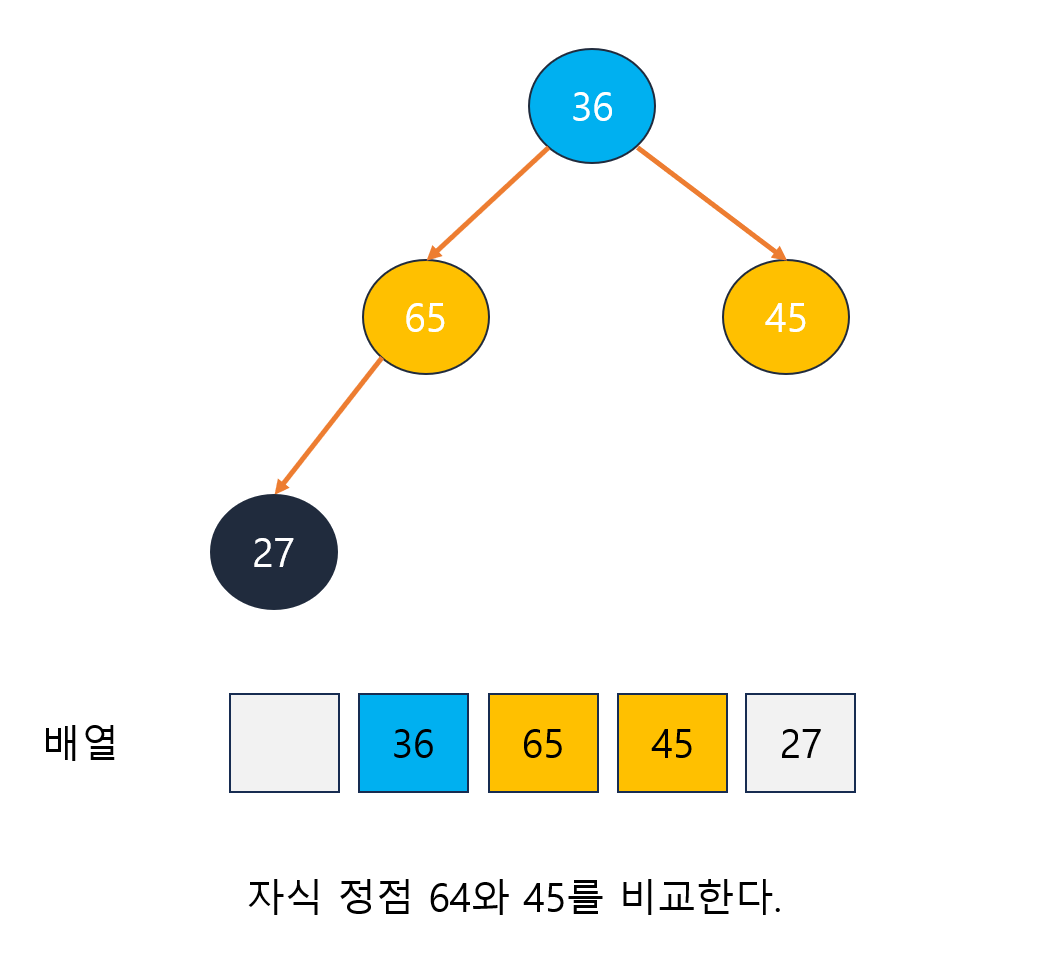
- 루트 정점의 두 자식 정점 중 더 우선순위가 높은 정점과 바꾼다.
- 두 자식 정점이 우선순위가 더 낮을 때 까지 반복한다.
- 완전 이진 트리의 높이는 Log N이기에 힙의 요소 제거 알고리즘은 O(log N) 시간 복잡도를 가진다.
힙의 요소 제거 과정
1.
2.

3.
4.
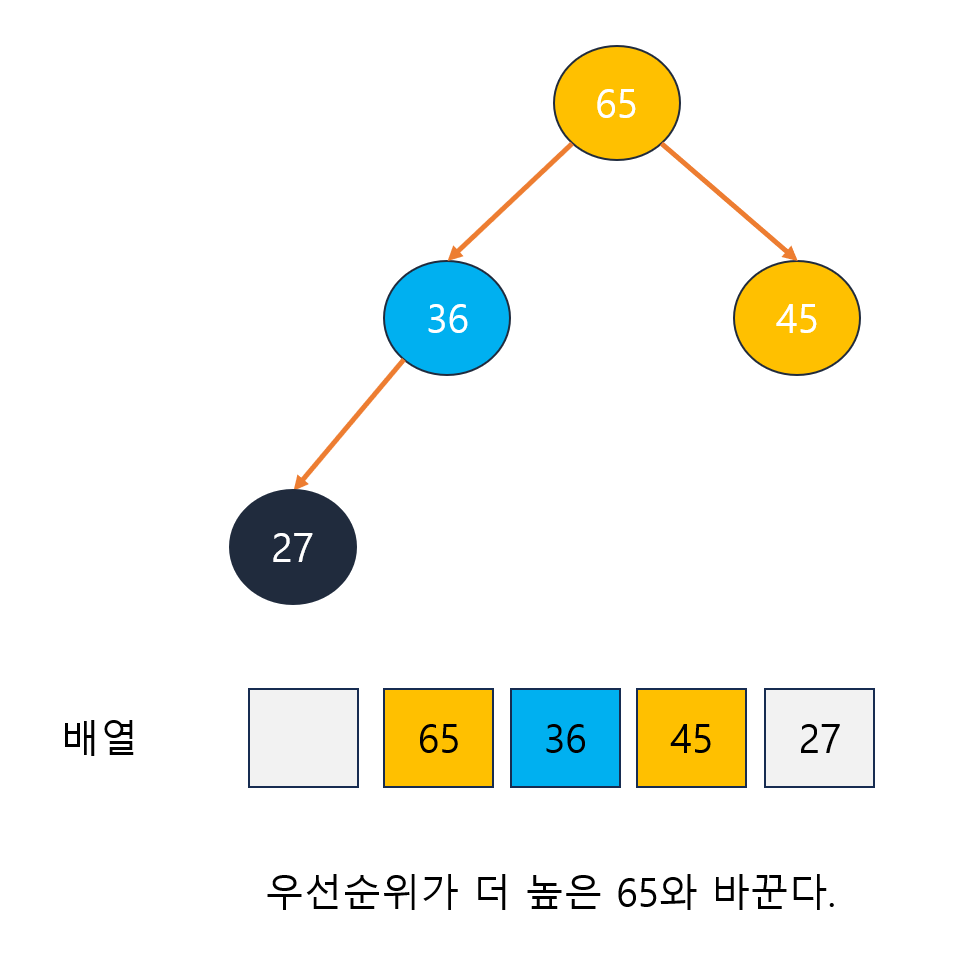
5.

6.
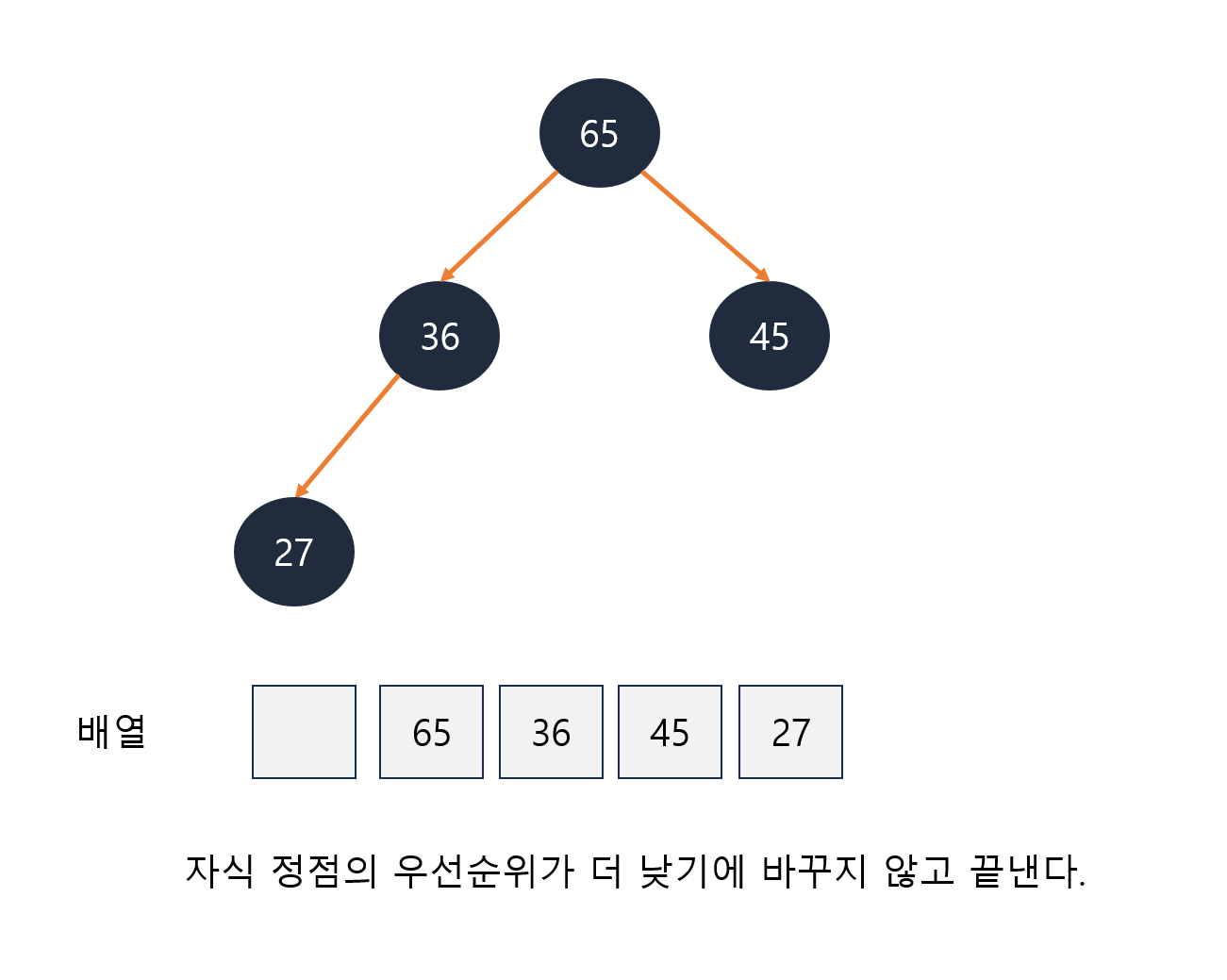
최대 힙
class MaxHeap {
//0번 인덱스는 편의를 위해 비어둔다.
constructor() {
this.heap = [null];
}
push(value){
//힙의 마지막에 추가하고 부모와 비교하기 위해 부모인덱스와 현재 인덱스를 구한다.
this.heap.push(value);
let currentIndex = this.heap.length-1;
let parentIndex = Math.floor(currentIndex / 2);
//부모가 더 우선순위가 낮거나 root가 아닐 때까지 반복
while (parentIndex !== 0 && this.heap[parentIndex] < value) {
const temp = this.heap[parentIndex];
this.heap[parentIndex] = value;
this.heap[currentIndex] = temp;
currentIndex = parentIndex;
parentIndex = Math.floor(currentIndex / 2)
}
}
pop () {
// 루트 요소를 반환하기위해 상수 저장
const returnValue = this.heap[1];
// 루트 정점을 가장 마지막 요소로 바꾼다.
this.heap[1] = this.heap.pop();
//루트로 부터 아래로 내려가기 위한 변수를 선언
let currentIndex = 1;
let leftIndex = 2;
let rightIndex = 3;
//반복은 하위 정점들이 현재 정점보다 우선순위가 낮을 때 종료한다.
while(
this.heap[currentIndex] < this.heap[leftIndex] ||
this.heap[currentIndex] < this.heap[rightIndex]
) {
// 왼쪽 정점 보다 오른쪽 정점이 우선순위가 높으면 오른쪽과 루트를 바꾼다.
if(this.heap[leftIndex] < this.heap[rightIndex]) {
const temp = this.heap[currentIndex];
this.heap[currentIndex] = this.heap[rightIndex];
this.heap[rightIndex] = temp;
currentIndex = rightIndex;
} else {
// 오른쪽 정점 보다 왼쪽 정점이 우선순위가 높으면 왼쪽과 바꾼다.
const temp = this.heap[currentIndex]
this.heap[currentIndex] = this.heap[leftIndex];
this.heap[leftIndex] = temp;
currentIndex = leftIndex;
}
// 바꾼 정점의 오른쪽 정점 위치와 왼쪽 정점의 위치를 바꿔준다.
leftIndex = currentIndex * 2
rightIndex = currentIndex * 2 + 1;
}
return returnValue;
}
}
const heap = new MaxHeap();
heap.push(45);
최소 힙
class MinHeap {
//0번 인덱스는 편의를 위해 비어둔다.
constructor() {
this.heap = [null];
}
push(value){
//힙의 마지막에 추가하고 부모와 비교하기 위해 부모인덱스와 현재 인덱스를 구한다.
this.heap.push(value);
let currentIndex = this.heap.length-1;
let parentIndex = Math.floor(currentIndex / 2);
//부모가 더 우선순위가 높거나 root가 아닐 때까지 반복
while (parentIndex !== 0 && this.heap[parentIndex] > value) {
const temp = this.heap[parentIndex];
this.heap[parentIndex] = value;
this.heap[currentIndex] = temp;
currentIndex = parentIndex;
parentIndex = Math.floor(currentIndex / 2)
}
}
pop () {
// 루트 요소를 반환하기위해 상수 저장
const returnValue = this.heap[1];
// 루트 정점을 가장 마지막 요소로 바꾼다.
this.heap[1] = this.heap.pop();
//루트로 부터 아래로 내려가기 위한 변수를 선언
let currentIndex = 1;
let leftIndex = 2;
let rightIndex = 3;
//반복은 하위 정점들이 현재 정점보다 우선순위가 높을 때 종료한다.
while(
this.heap[currentIndex] > this.heap[leftIndex] ||
this.heap[currentIndex] > this.heap[rightIndex]
) {
// 왼쪽 정점 보다 오른쪽 정점이 우선순위가 낮으면 오른쪽과 루트를 바꾼다.
if(this.heap[leftIndex] > this.heap[rightIndex]) {
const temp = this.heap[currentIndex];
this.heap[currentIndex] = this.heap[rightIndex];
this.heap[rightIndex] = temp;
currentIndex = rightIndex;
} else {
// 오른쪽 정점 보다 왼쪽 정점이 우선순위가 낮으면 왼쪽과 바꾼다.
const temp = this.heap[currentIndex]
this.heap[currentIndex] = this.heap[leftIndex];
this.heap[leftIndex] = temp;
currentIndex = leftIndex;
}
// 바꾼 정점의 오른쪽 정점 위치와 왼쪽 정점의 위치를 바꿔준다.
leftIndex = currentIndex * 2
rightIndex = currentIndex * 2 + 1;
}
return returnValue;
}
}
const heap = new MinHeap();
heap.push(45);
'TIL' 카테고리의 다른 글
| [2023-09-26] TIL - 자료구조 & 알고리즘 - 정렬 (0) | 2023.09.27 |
|---|---|
| [2023-09-26] TIL - 자료구조 & 알고리즘 - 트라이(Trie) (0) | 2023.09.26 |
| [2023-09-26] TIL - 자료구조 & 알고리즘 - 트리 (0) | 2023.09.26 |
| [2023-09-25] 자료구조 & 알고리즘 - 그래프 (0) | 2023.09.25 |
| [2023-09-25] 자료구조 & 알고리즘 - 해시테이블 (0) | 2023.09.25 |