Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 코딩테스트
- 리액트댓글기능
- 다이나믹프로그래밍
- JS프로그래머스
- 리액트
- 백준골드
- 프로그래머스
- 익스프레스
- 백준알고리즘
- 알고리즘
- 프로그래머스코테
- 리액트커뮤니티
- 프로그래머스JS
- 포이마웹
- HTML
- 몽고DB
- js코테
- css기초
- 백준nodejs
- 백준js
- CSS
- JS
- 백준
- 코테
- 백준구현문제
- HTML5
- dp알고리즘
- 자바스크립트
- 안드로이드 스튜디오
- 백준구현
Archives
- Today
- Total
개발새발 로그
[2023-09-27] TIL - 자료구조 & 알고리즘 - 이진탐색 본문
선형 탐색
- 순서대로 하나씩 찾는 알고리즘
- O(n) 시간 복잡도가 걸린다.
이진 탐색
- 정렬되어 있는 요소들을 반씩 제외하며 찾는 알고리즘
- O(log n)만큼 시간복잡도가 걸린다.
이진 탐색의 특징
- 반드시 정렬이 되어있어야 사용할 수 있다.
- 배열 혹은 이진트리를 이용하여 구현할 수 있다.
- O(log n) 시간복잡도인 만큼 상당히 빠르다.
배열을 이용한 구현 방법
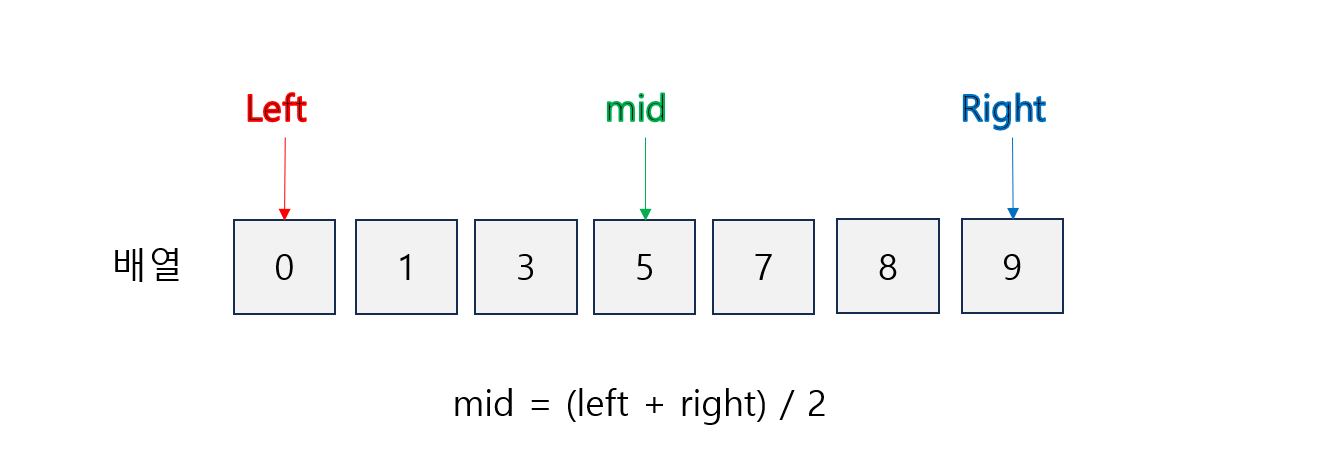
이진 탐색 트리를 이용한 구현 방법
- 배열을 이용한 방법은 중간에 요소를 추가하거나 삭제하는 경우에는 선형시간이 걸린다는 단점이 여전히 존재한다.
- 이 단점을 해결하기 위해 이진 탐색 트리를 이용한다.
이진 탐색 트리
- 이진 탐색을 위한 이진트리로 왼쪽 서브트리는 루트보다 작은 값이 모여있고, 오른쪽 서브트리는 루트보다 큰 값이 모여있다.
이진 탐색 트리 요소 추가
1.
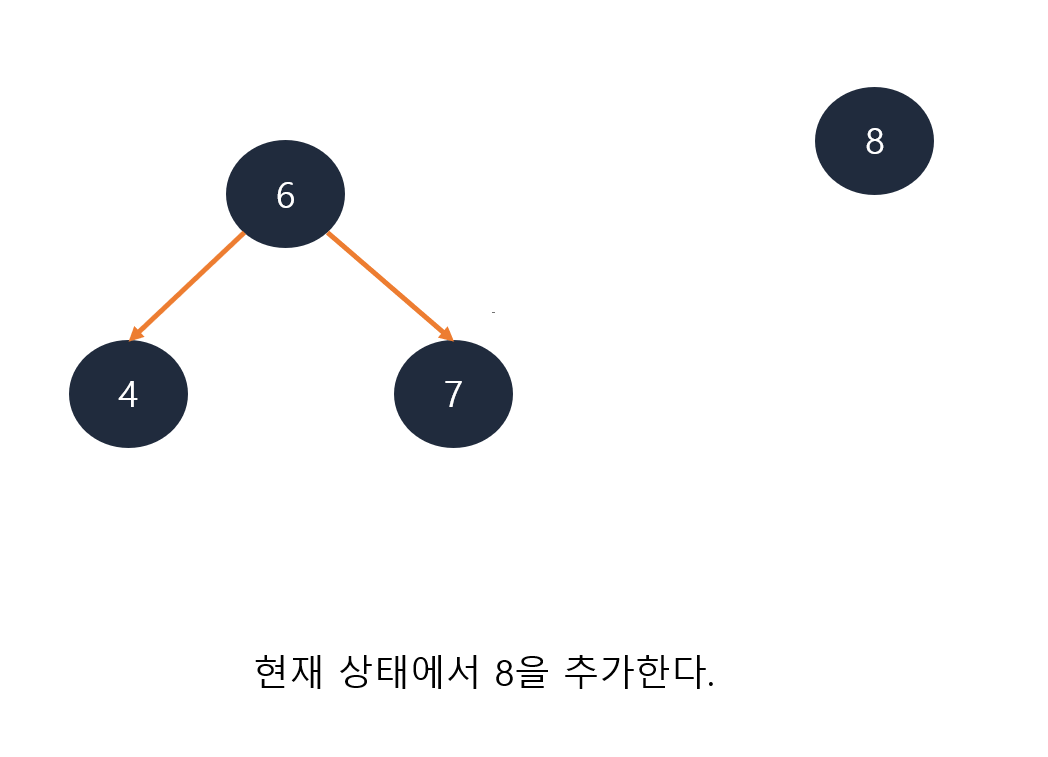
2.
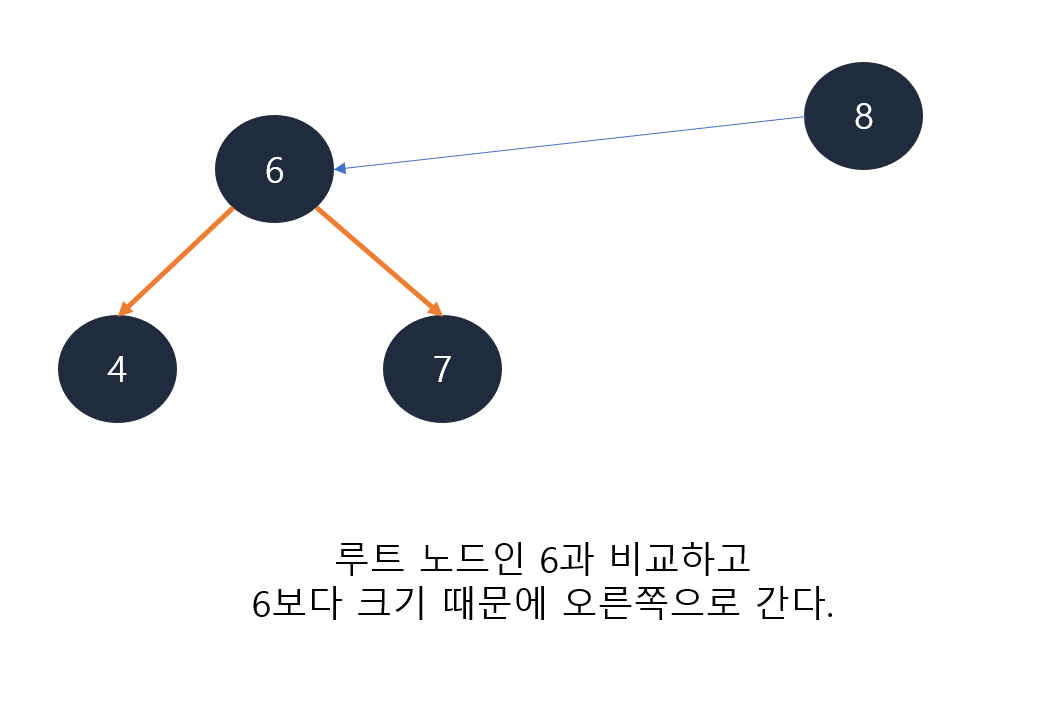
3.
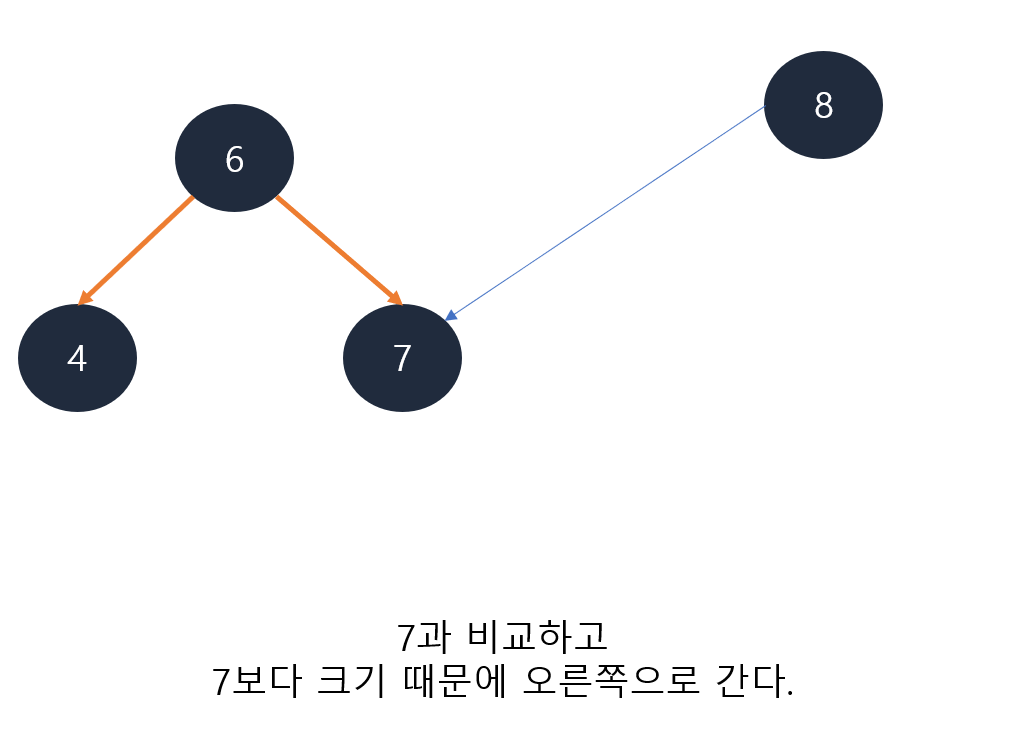
4.
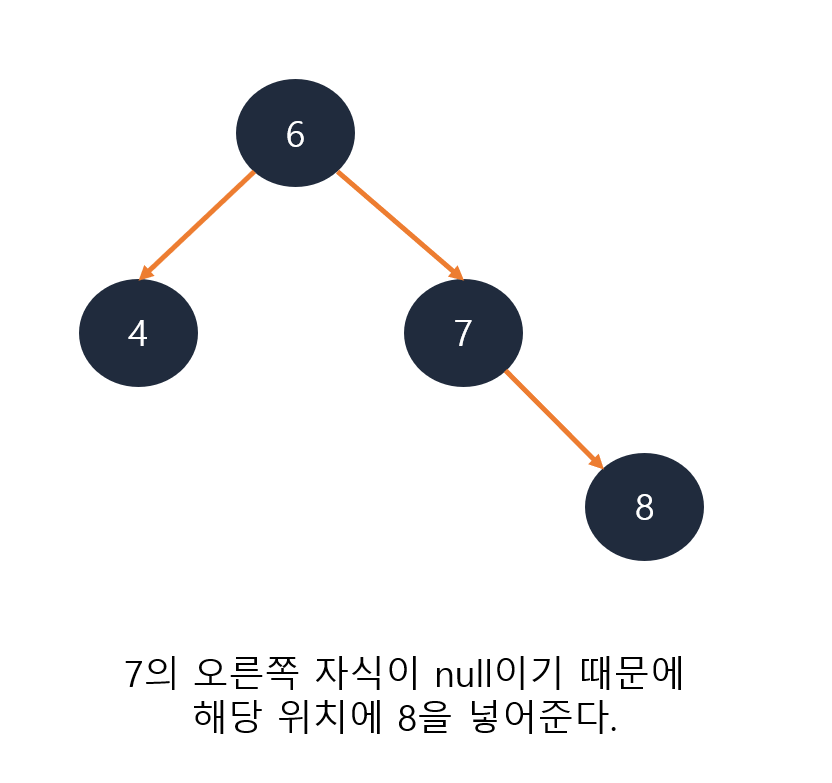
이진 탐색 트리 요소 삭제
-삭제에서는 3가지의 경우가 존재한다.
1. 단말 정점을 삭제하는 경우
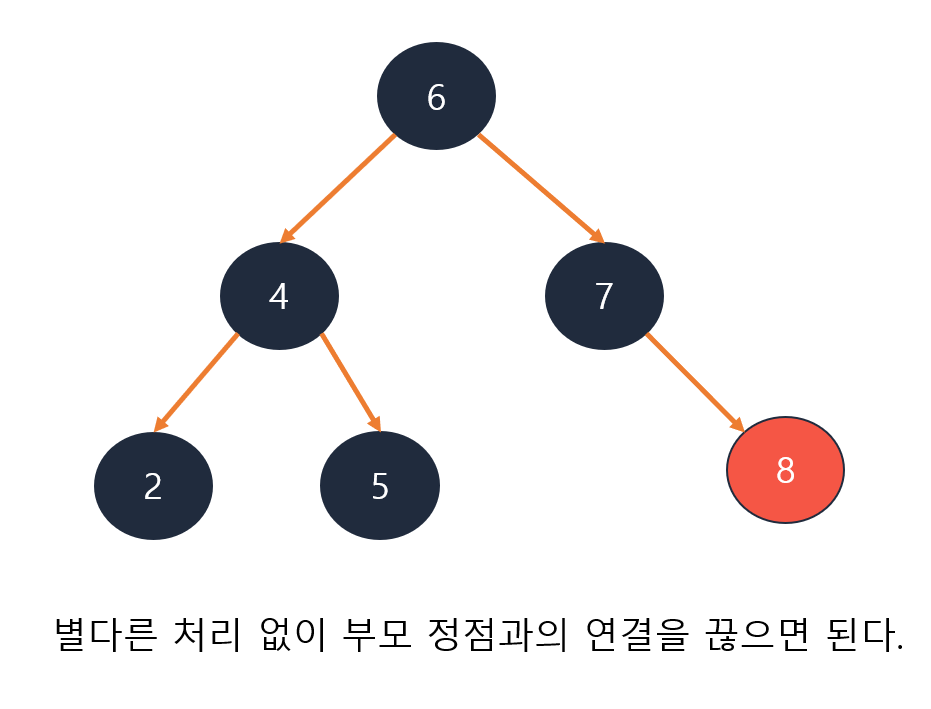
2. 하나의 자식을 가지는 경우
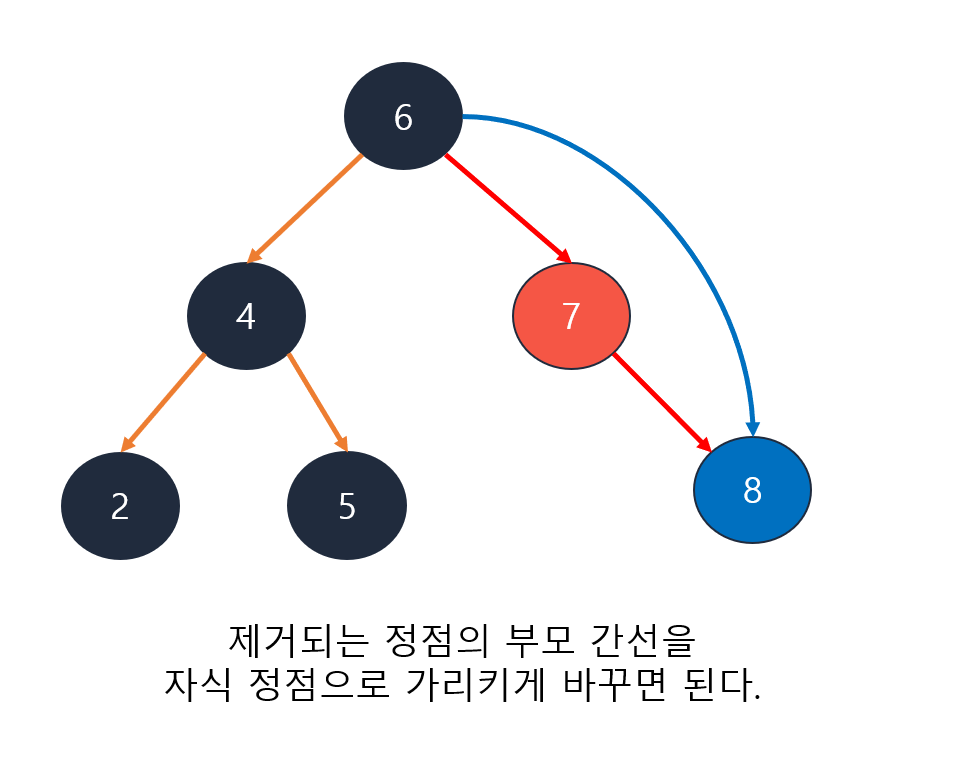
3. 두 개의 자식을 가지는 경우
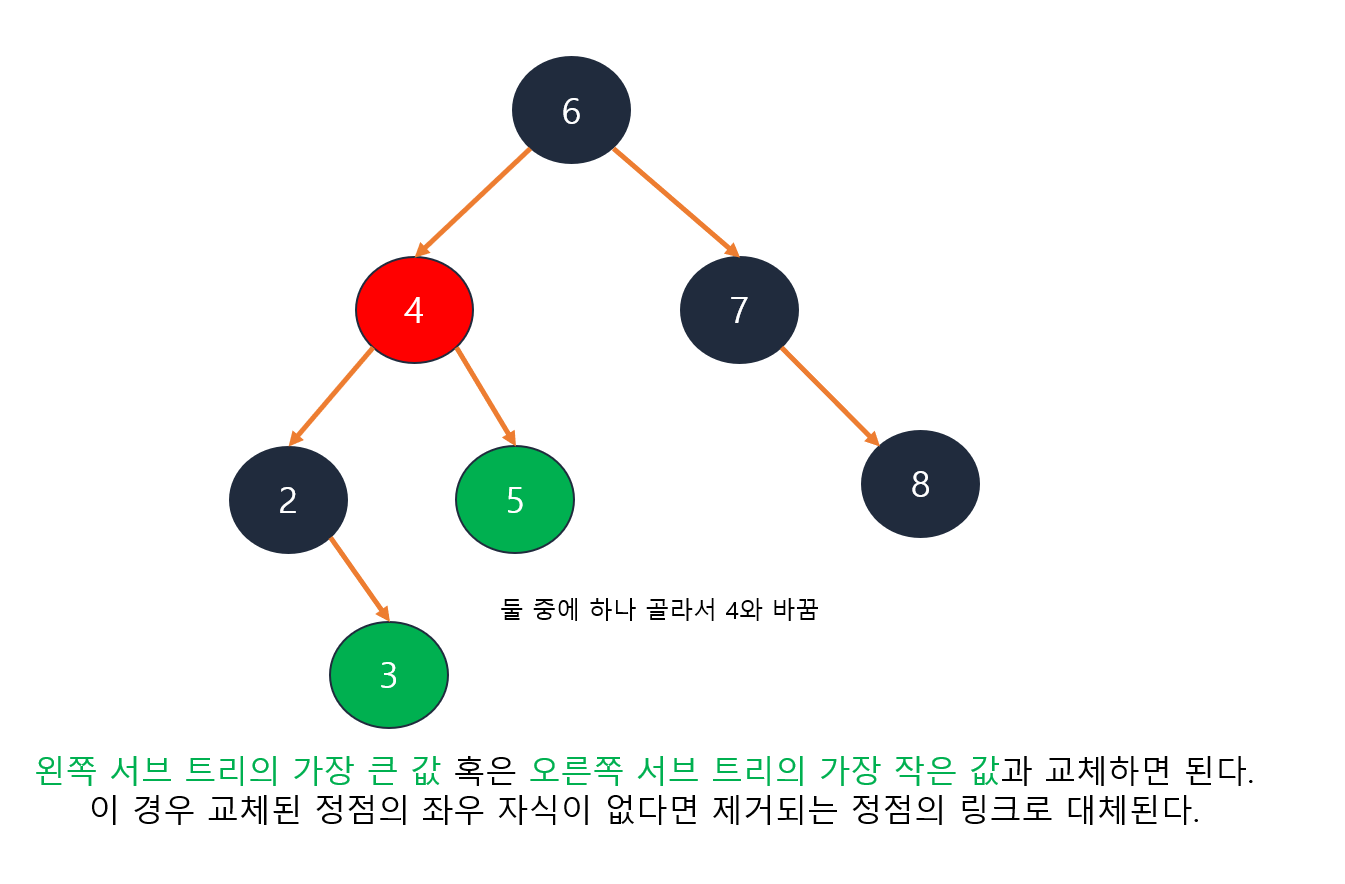
이진 탐색 트리의 문제점
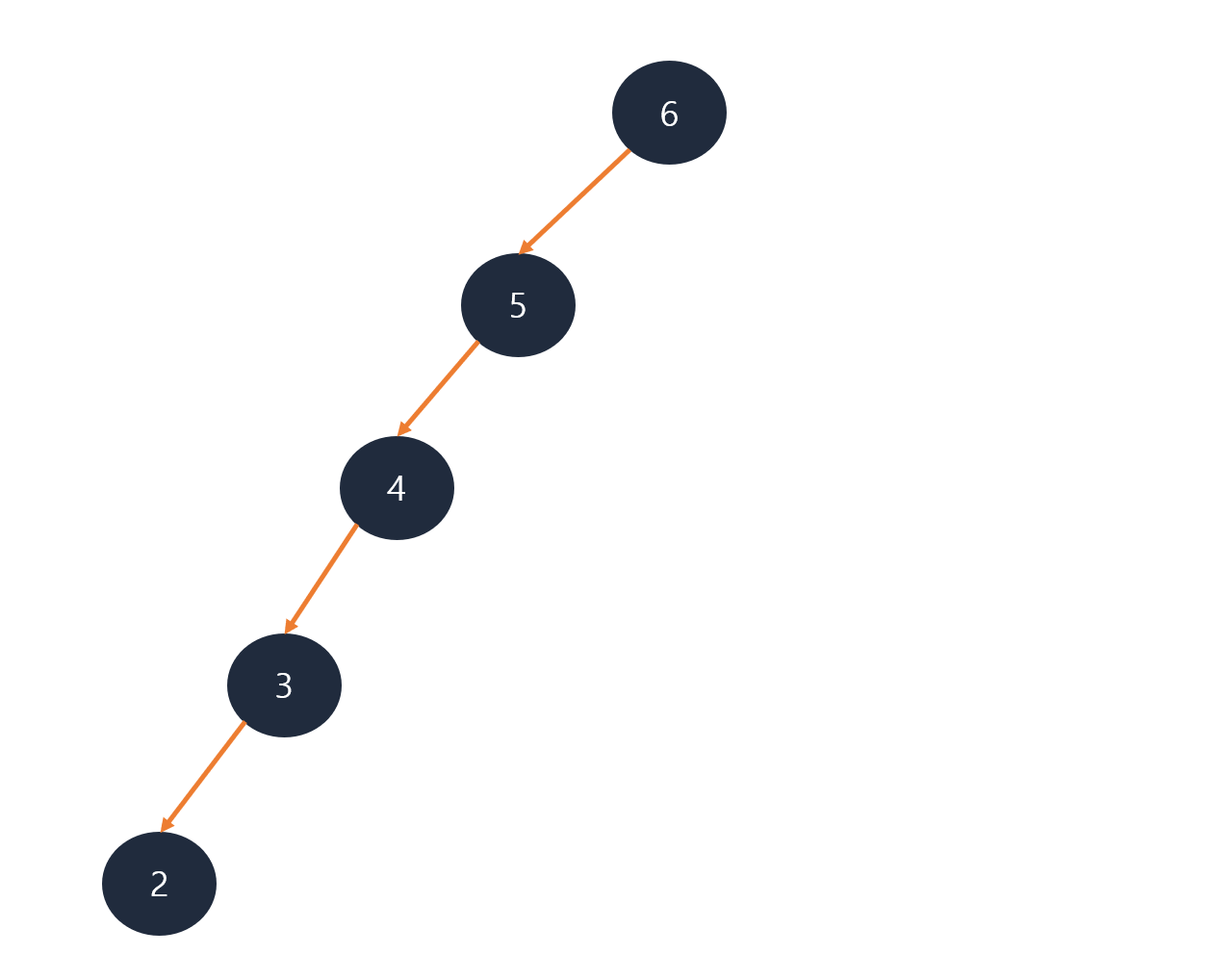
- 최악의 경우 한쪽으로 편향된 트리가 될 수 있다.
- 그런 경우 순차탐색과 동일한 시간복잡도를 가진다.
- 아를 해결하기 위해 다음과 같은자료구조를 이용할 수 있다.
- AVL 트리
- 레드 블랙 트리
자바스크립트에서 사용법
- 배열을 이용한 방법
const array = [1, 1, 5, 134, 400, 599, 1004, 2876, 8712];
function binarySearch(array, findValue){
let left = 0;
let right = array.length - 1;
let mid = Math.floor((left + right) / 2);
//값을 찾을 때까지 반복
while(left < right){
if(array[mid] === findValue)
return mid;
if(array[mid] < findValue)
left = mid + 1;
else
right = mid - 1;
mid = Math.floor((left + right) / 2);
}
//루프를 중간에 빠져나오지 못했다면 -1을 반환
return -1;
}
console.log(binarySerach(array,2876)); // 7
console.log(binarySerach(array,1)); // 0
console.log(binarySerach(array,500)); // -1
- 이진 탐색 트리(제거 함수 추가)
// 기존 이진 트리에 탐색을 추가함
class Node {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor() {
this.root = null;
}
insert(value) {
const newNode = new Node(value);
//루트가 비어있으면 추가한 노드가 정점
if (this.root === null) {
this.root = newNode;
return;
}
// 현재 노드가 null이 아닐 때까지 루프를 돌린다.
let currentNode = this.root;
while (currentNode !== null) {
// 만약 루트 값보다 추가한 값이 더 크다면
if (currentNode.value < value) {
//오른쪽이 비어있다면 오른쪽에 넣는다.
if (currentNode.right === null) {
currentNode.right = newNode;
break;
}
//비어있지 않다면 현재 노드를 다음 오른쪽 정점으로 바꿔준다.
currentNode = currentNode.right;
} else {
//만약 루트값이 추가한 값보다 작거나 같고
// 왼쪽 정점이 비어있다면
if (currentNode.left === null) {
//왼쪽 정점에 추가한 노드를 넣어준다.
currentNode.left = newNode;
break;
}
//비어있지 않다면 현재 노드를 다음 왼쪽 정점으로 바꿔준다.
currentNode = currentNode.left;
}
}
}
// 탐색
has(value) {
let currentNode = this.root;
// 현재 노드가 null일 때까지 반복
while (currentNode !== null) {
//현재 노드 값이 찾는 값이라면 true반환
if (currentNode.value === value) {
return true;
}
// 찾는 값이 현재 노드보다 크다면
if (currentNode.value < value) {
//오른쪽 정점으로 이동
currentNode = currentNode.right;
} else {
// 찾는 값이 현재 노드보다 작거나 같다면 왼쪽 정점으로 이동
currentNode = currentNode.left;
}
}
//못찾았다면 false반환
return false;
}
remove(value) {
let currentNode = this.root;
let parentNode = null;
while (currentNode) {
//만약 삭제할 값을 찾았다면
if (value === currentNode.value) {
// 1. 리프노드일 경우
if (!currentNode.left && !currentNode.right) {
if (!parentNode) {
this.root = null;
} else {
if (currentNode.value < parentNode.value) {
parentNode.left = null;
} else {
parentNode.right = null;
}
}
}
// 2. 자식노드가 right 하나인 경우
else if (!currentNode.left) {
if (!parentNode) {
this.root = currentNode.right;
} else {
if (currentNode.value < parentNode.value) {
parentNode.left = currentNode.right;
} else {
parentNode.right = currentNode.right;
}
}
}
// 2. 자식노드가 left 하나인 경우
else if (!currentNode.right) {
//만약 부모노드가 없다면 현재 노드가 루트 노드인 경우임
if (!parentNode) {
// 현재 노드가 루트 노드이니까 남은 left 하나를 루트 노드로 만듦
this.root = currentNode.left;
} else {
// 현재 찾은 노드의 값이 부모의 값보다 작다면
if (currentNode.value < parentNode.value) {
// 부모의 left는 현재 노드의 left로 만든다.
// 왜냐하면 현재 노드를 제거하면
// 그 하위 노드의 값이 크면 오른쪽 작으면 왼쪽으로 가야하기 때문이다.
parentNode.left = currentNode.left;
} else {
parentNode.right = currentNode.left;
}
}
}
// 3. 자식 노드를 두 개 가진 경우
else {
// 원래는 왼쪽 노드 중 가장 큰 값이나 오른쪽 노드에서 가장 작은 값 중 하나를 제거한 위치에 넣는 것이다.
// 여기서는 항상 오른쪽 노드에서 가장 작은 값을 삭제한 위치에 둘 것이다.
//먼저 현재노드에서 오른쪽 노드 값을 가져온다.
let minValueNode = currentNode.right;
let minValueNodeParent = currentNode;
//오른쪽 노드의 왼쪽 노드가 가장 작은 값이므로
//오른쪽 노드에서 가장 작은 값이 나올 때 가지 반복한다.
while (minValueNode.left) {
minValueNodeParent = minValueNode;
minValueNode = minValueNode.left;
}
//가장 작은 값을 현재 노드의 값으로 바꿔준다.
currentNode.value = minValueNode.value;
// 그리고 가장 작은 값인 노드를 삭제해줘야한다.
// 가장 작은 값이 노드를 삭제하면 그 노드에 연결되어있던 자식노드가 있을 수 있다.
// 하지만 가장 작은 값이므로 왼쪽 자식은 존재하지 않을 것이고, 오른쪽 자식이 존재할 수도, 안할 수도 있다.
if (minValueNodeParent.left === minValueNode) {
// 삭제한 노드 값이 만약 부모노드의 왼쪽 자식이라면
// 현재 부모노드의 왼쪽에 minValueNode.right를 둬야한다.
minValueNodeParent.left = minValueNode.right;
} else {
// 만약 가장 작은 값인 노드가 이전 노드의 오른쪽자식이였다면
// 가장 작은 값이 있던 위치에는 가장 작은 값의 오른쪽 자식으로 바뀌게 된다.
//이 경우는 루트에서 처음에 오른쪽 자식으로 갔을 때의 경우 때문이다.
minValueNodeParent.right = minValueNode.right;
}
}
return console.log("삭제를 완료했습니다.");
} else if (value < currentNode.value) {
parentNode = currentNode;
currentNode = currentNode.left;
} else {
parentNode = currentNode;
currentNode = currentNode.right;
}
}
return console.log("삭제를 수행할 수 없습니다.");
}
}
const tree = new BinarySearchTree();
tree.insert(5);
tree.insert(4);
tree.insert(7);
tree.insert(8);
tree.insert(5);
tree.insert(6);
tree.insert(2);
console.log(tree.has(8));
tree.remove(8);
console.log(tree.has(8));
프로그래머스 코딩테스투
https://school.programmers.co.kr/learn/courses/30/lessons/43238?itm_content=course14743
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
내 제출
function solution(n, times) {
times.sort((a,b)=>a-b);
let lt=1;
let rt=times[times.length-1]*n
let answer = rt;
while(lt<=rt){
let mid=Math.floor((lt+rt)/2);
let count = 0
//각 심사관이 mid시간안에 몇명을 심사할 수 있는지 각각 값을 누적한다.
//이때 심사할 인원 n보다 커지면 그 시간안에는 무조건 가능하다는 뜻이므로
//모든 반복문이 돌지 않아도 n보다 커질때 반복이 멈춰야한다.
times.forEach(value => {
count += Math.floor(mid / value); // 한 사람당 몇명 할 수 있는지
if(count >= n) { //n보다 커지면 그 시간안에는 무조건 심사가 모두 가능하니까 반복 중간에 멈춤
answer = Math.min(mid, answer); // 최솟값
return;
};
});
//만약에 n보다 누적명수가 크면 mid시간보다 적게도 가능한거니까 rt를 줄인다.
if (count >= n) {
rt = mid - 1;
}
//만약에 반복을 모두 돌아도 n보다 작으면 n명을 심사할 시간이 부족하므로 lt를 증가한다.
else {
lt = mid + 1;
}
}
return answer;
}
다른 풀이
function solution(n, times) {
times.sort((a,b)=>a-b);
let lt=1;
let rt=times[times.length-1]*n
let answer = rt;
while(lt<=rt){
let mid=Math.floor((lt+rt)/2);
const sum = times.reduce((acc,time) => acc + Math.floor(mid / time),0));
if (sum >= n) {
rt = mid - 1;
}
else {
lt = mid + 1;
}
}
return lt;
}
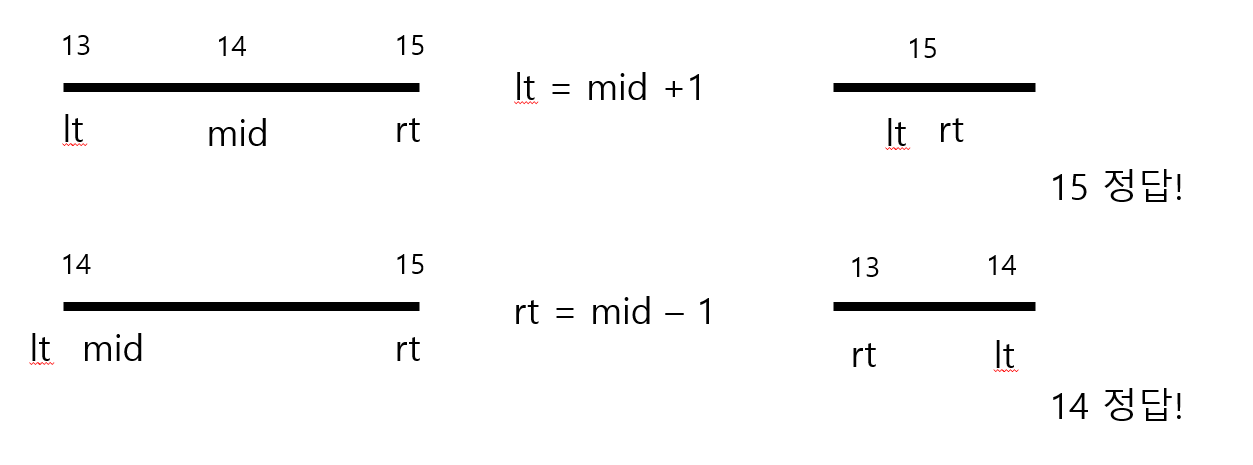
728x90
반응형
LIST
'TIL' 카테고리의 다른 글
| [2023-09-27] TIL - 그리디 (0) | 2023.09.27 |
|---|---|
| [2023-09-27] 자료구조 & 알고리즘 - BFS,DFS (0) | 2023.09.27 |
| [2023-09-26] TIL - 자료구조 & 알고리즘 - 정렬 (0) | 2023.09.27 |
| [2023-09-26] TIL - 자료구조 & 알고리즘 - 트라이(Trie) (0) | 2023.09.26 |
| [2023-09-26] 자료구조 & 알고리즘 - 힙 (0) | 2023.09.26 |