| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 백준nodejs
- 백준알고리즘
- 포이마웹
- 프로그래머스코테
- 프로그래머스JS
- 다이나믹프로그래밍
- 백준
- 자바스크립트
- 백준구현
- CSS
- JS프로그래머스
- dp알고리즘
- HTML
- 백준js
- 리액트댓글기능
- 프로그래머스
- 리액트
- 백준골드
- 코딩테스트
- 안드로이드 스튜디오
- 백준구현문제
- JS
- 몽고DB
- 코테
- 익스프레스
- 리액트커뮤니티
- 알고리즘
- HTML5
- js코테
- css기초
- Today
- Total
개발새발 로그
다익스트라 알고리즘 본문
다익스트라 알고리즘은 다이나믹 프로그래밍을 활용한 최단경로탐색 알고리즘입니다.
이전에 배운 크루스칼 알고리즘은 최소비용 신장트리이다.
다른점은 크루스칼은 모든정점이 연결될 때의 최소비용이고
다익스트라는 특별한 정점에서 다른 모든 정점으로 가는 최단 경로다.
즉 크루스칼은 모든 정정이 연결만 되면 되는 경우이고,
다익스트라는 어떤 정점을 기준으로 모든 정점을 도착지점으로 했을 때 갈 수 있는 최소비용을 구하는 것이다.
다익스트라 알고리즘은 특정한 정점에서 다른 모든 정점으로 가는 최단 경로를 구합니다.
이때 음의간선은 포함할 수 없는데 이것이 다익스트라가 현실세계에서 사용하기 매우 적합한 알고리즘 중 하나입니다.
다익스트라가 다이나믹 프로그래밍이기도 하고, 그리디 알고리즘으로 분류되기도 한다.
다이나믹 프로그래밍 문제인 이유는 최단거리는 여러개의 최단거리로 이루어져 있기 때문입니다.
다익스트라의 특징은 하나의 최단 거리를 구할 때 그 이전 까지 구했던 최단 거리 정보를 그대로 사용한다는 점이다.

기본적으로 노드 1부터 갈 수있는 노드의 최단거리를 산정해야한다.
1에서는 2와 4, 5를 갈 수 있다.
컴퓨터는 하나씩 계산할 수 밖에 없습니다.
그래서 1에서 2로 가는 최소비용은 5입니다. 거리가 6이기 때문입니다.

이제 1에서 갈 수 있는 최소비용중 가장 최단 거리는 3이므로 다음 노드는 4를 처리하게 된다.
이때 컴퓨터는 1 -> 5의 비용이 12인데 1 -> 4 -> 5의 비용은 10으로 더 저렴하다는 것을 알 게 됩니다.
이 때 현재까지 컴퓨터가 알고있던 5로 가는 최소비용 12를 새롭게 10으로 갱신하는 것입니다.
즉 현재까지 알고 있던 최단 경로를 계속해서 갱신합니다.
구체적인 작동과정
- 출발노드 설정
- 출발노드를 기준으로 각 노드의 최소비용을 저장
- 방문하지 않은 노드 중에서 가장 비용이 적은 노드를 선택
- 해당 노드를 거쳐서 특정한 노드로 가는 경우를 고려하여 비용을 갱신
- 3 ~ 4번 과정을 반복
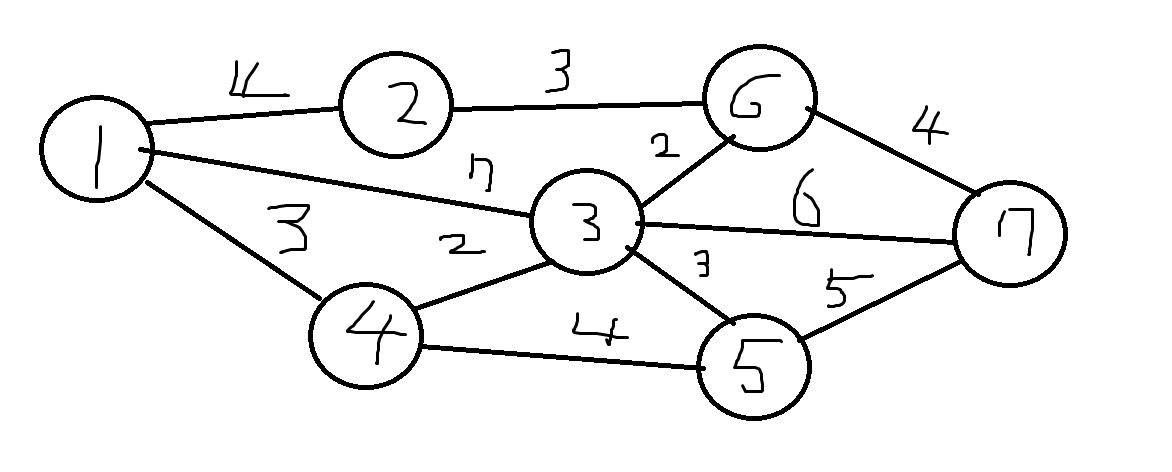
이 그래프를 이용해보자. 이러한 그래프느 실제로 컴퓨터에서 처리할 때 이차원배열형태로 처리해야한다.
배열의 값은 행에서 열로 가는 비용을 의미한다.
| 0 | 4 | 7 | 3 | Infinity | Infinity | Infinity |
| 4 | 0 | Infinity | Infinity | Infinity | 3 | Infinity |
| 7 | Infinity | 0 | 2 | 3 | 2 | Infinity |
| 3 | Infinity | 2 | 0 | 4 | Infinity | Infinity |
| Infinity | Infinity | 3 | 4 | 0 | Infinity | 5 |
| Infinity | 3 | 2 | Infinity | Infinity | 0 | 4 |
| Infinity | Infinity | 6 | Infinity | 5 | 4 | 0 |
1행 2열은 1에서 2로가는 비용을 적은 것이다.

이제 1 노드를 선택하고 그에 연결된 간선 3개를 확인한 상태이다. 1번에서 다른 노드로 가는 정점의 최소비용은 다음과 같다. (현재 주황색 배경이 방문했다는 뜻이다.)
| 0 | 4 | 7 | 3 | Infinity | Infinity | Infinity |
현재 방문하지 않은 노느중에서 가장 비용이 적은 노드는 4번이다.
그래서 다음 노드는 4번 노드가 선택된다.
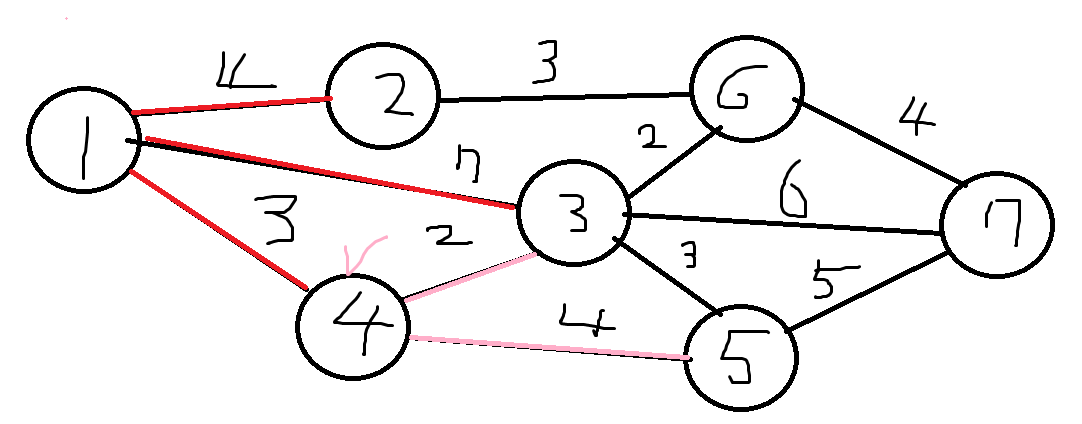
이제 1에서 4로가는 비용 3을 받아서 노드 3과 5로 가는 비용에 더한다.
그러면 1 -> 4 - > 3의 비용은 5가되고
1 -> 4 -> 5 의 비용은 7이 된다.
이때 1에서 3번을 가는 비용과 5번을 가는 비용을 확인한다.
1에서 3으로 가는 비용은 7로 1->4->3의 비용 5가 저렴하므로 5로 갱신된다.
1에서 5로가는 비용은 infinity로 1->4->5의 비용 7이 저렴해 7로 갱신된다.
| 0 | 4 | 5 | 3 | 7 | Infinity | Infinity |
이제 그 다음에 다시 1에서 방문하지 않은 노드 중 비용이 가장 적은 노드는 2번노드이다.
만약 노드 방문하지 않은 노드 중 가장 적은 비용이 드는 노드가 두 개 이상이라면 앞에 있는 노드부터 차례로한다.

이때 2번노드로 갈 수 있는 노드는 6번으로
1번에서 비용 4를 받아와 3에 더한다.
그럼 1->6번으로 가는 비용은 infinity에서 7로 갱신된다.
| 0 | 4 | 5 | 3 | 7 | 7 | Infinity |
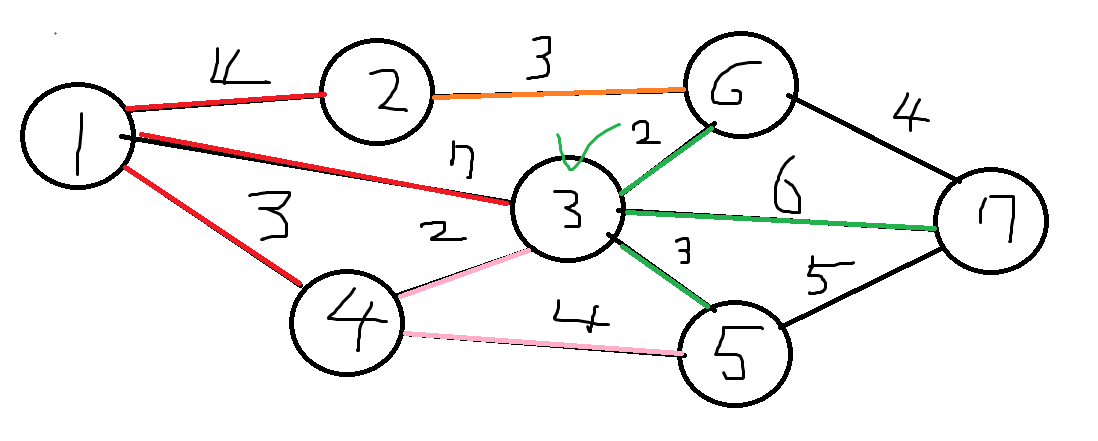
다음으로 방문하지 않은 노드중에서 가장 비용이 적은 노드는 3번째 노드이다.
3번에서는 5번 6번7 번을 갈 수있다.
3번으로 갈 수 있는 최소 비용은 5이다.
이제 이제 3번노드를 거쳐서 6을 가는 비용을 계산해보자.
5 + 2 = 7 이다.
기본에 1에서 2번노드를 거쳐 가는 비용이 7로 갱신되어있었다.
같으므로 패스한다.
그리고 3번노드를 거쳐서 6을 가는 비용을 계산하자
5 + 2 =7 이다.
기존에 1번에서 6번노드로 가는 비용이 7로 같다.
같으므로 패스한다.
이제 3번노드를 거쳐 7번으로 가는 비용을 계산한다.
5 + 6 = 11이다.
기존에 1번에서 7번노드로 가는 값은 infinity로 11보다 크다.
11이 작으므로 11로 갱신해준다.
| 0 | 4 | 5 | 3 | 7 | 7 | 11 |

다음으로 방문하지 않은 노드중 가장 작은 비용은 5번노드와 6번노드이다. 이때 앞에서부터 선택하여 5번노드가 다음노드가 된다.
5번노드에서 갈 수 있는 노드는 7번노드이다.
5번노드를 거쳐서 7번노드로 가는 비용은
7 + 5 =12 이다.
기존의 값 11보다 비싸므로 패스한다.
| 0 | 4 | 5 | 3 | 7 | 7 | 11 |
다음으로 가장 작은 비용인 6번노드가 선택된다.

6번노드에서 갈 수 있는 노드는 7번이다.
6번노드를 거쳐서 7번노드로 가는 비용은
7 + 4 = 11이다.
1에서 7번노드로 가는 값이 현재 11이므로 같으니까 패스한다.
| 0 | 4 | 5 | 3 | 7 | 7 | 11 |
이제 마지막 7번노드를 선택한다.

노드를 방문한 뒤에도 결과는 같으므로 최종 배열은 다음과 같습니다.
| 0 | 4 | 5 | 3 | 7 | 7 | 11 |
이 값이 1에서부터 출발해서 각각 노드로 갈 수 있는 최소비용이 된다.
이제 코드로 작성해보자
let number = 7 //정점의 갯수
let INF = 10000000; //무한대의 값 초기화
//전체 그래프를 초기화한다.
const arr = [
[ 0 , 4, 7, 3, INF, INF, INF],
[ 4, 0, INF, INF, INF, 3, INF],
[ 7, INF, 0, 2, 3, 2, INF],
[3, INF, 2, 0, 4, INF, INF],
[INF, INF, 3, 4, 0, INF, 5],
[INF, 3, 2, INF, INF, 0, 4],
[INF, INF, 6, INF, 5, 4, 0]
];
//방문됐는지 확인하는 배열
const isVisit = Array.from({length:7},()=>false);
//최단거리를 저장할 배열
var d = Array.from({length:7},()=>0);
//가장 최소 거리를 가지는 정점을 반환한다.
//방문할 노드를 정하는 로직(앞에서부터 한개씩 검사해서 가장 비용이 적은 노드를 찾음
//선형탐색
const getMin = function(v){
let min =INF;
let idx=0;
for(let i=0;i<number;i++){
//방문하지 않은노드 중에서 현재 최소값보다 더 작으면 그값이 min이된다.
if(min>d[i] && !isVisit[i]){
min=d[i];
//그리고 그때의 위치를 기억한다.
idx=i;
}
}
return idx;
}
//다익스트라를 수행하는 함수
//특정한 정점에서 다른 노드로 갈 수 있는 최소비용을 구하는 로직
const dist = function(start){
//방문한 노드에서 갈 수있는 모든 정점의 거리를 저장
for(var i=0;i<number;i++){
d[i]=arr[start][i];
}
//시작점은 방문을 했음을 저장
isVisit[start]=true;
//number-2까지 가면서
for(var i=0;i<number-2;i++){
//현재 갈 수 있는 정점중 가장 비용이 적은 노드 저장
let current = getMin();
//그 노드 방문처리
isVisit[current]=true;
//그 노드에 인접한 모든 노드를 확인하면서
for(var j=0;j<number;j++){
//방문하지 않은 노드라면
if(!isVisit[j]){
//start에서 방문한 노드까지의 거리 + 방문한 노드에서 갈 수있는 정점의 거리
//즉 1이 start면 1 -> 3 -> 4
//그리고 start에서 방문한 노드에서 갈 수있는 정점의 거리를 비교
//즉 1-> 4
if(d[current]+arr[current][j] < d[j]){
d[j] = d[current] + arr[current][j]; //만약 기존께 크면 갱신
}
}
}
}
}
dist(0);
for(var i=0;i<number;i++){
console.log(d[i]);
}
하지만 실제로 이걸 사용하면 선형탐색이라서 O(N^2)이 된다.
최대한 빠르게 작동시켜야하므로 힙 구조를 이용해야한다.
// 0번 노드는 사용하지 않는 빈 노드이다.
// 이는 시작 노드를 1번으로 설정하기 위함이다.
const graph = [
[], // 사용X
[
{ to: 4, dist: 3 },//1에서 4
{ to: 2, dist: 4 }, //1에서 2
{ to: 3, dist: 7 }, //1에서 3
],
[
{ to: 6, dist: 3 } //2에서 6
],
[
{ to: 5, dist: 3 }, //3에서 5
{ to: 6, dist: 2 },//3에서 6
{ to: 7, dist: 6 },//3에서 7
],
[
{ to: 3, dist: 2 },//4에서 3
{ to: 5, dist: 4 },//4에서 5
],
[
{ to: 3, dist: 3 },//5에서 3
{ to: 7, dist: 5 }, //5에서 7
],
[
{ to: 3, dist: 2 },//6에서 3
{ to: 7, dist: 4 }, //6에서 7
],
[
{ to: 3, dist: 4 },//7에서 3
{ to: 6, dist: 6 }, //7에서 6
{ to: 5, dist: 5 },//7에서 5
],
];
// 1번 노드와 각 노드까지 최단 경로를 저장하는 배열 생성
const dist = Array(graph.length).fill(Infinity);
// 큐 생성 및 1번 노드에 대한 정보 저장
//1에서 1은 0이니까
const queue = [{ to: 1, dist: 0 }];
// 1번 노드의 거리는 0 으로 설정
//1에서 1은 0이ㅣㄴ까
dist[1] = 0;
// 큐가 빌 때까지 반복
while (queue.length) {
// 큐에서 방문할 노드 꺼내기
const { to } = queue.pop();
// 방문한 노드까지 이동한 거리 + 다음 방문 노드까지 거리를
// 기존에 저장된 값과 비교해서 갱신
//1에있느 2,3,4 순회
graph[to].forEach((next) => {
//acc는 1의 dist값과 1->2의 dist값을 더함
const acc = dist[to] + next.dist;
if (dist[next.to] > acc) {//만약 dist[1]의 값이 1에서 2의 경로값보다 크면
dist[next.to] = acc; //dist[2]을 갱신해줌
// 최단 경로가 되는 노드는 큐에 추가
// 최단경로인 이유는 갱신을 해줬으니까 가장 가깝다는 소리
//그래서 그 경로를 queue에 넣어줌
queue.push(next);
}
});
}console.log(dist)
연습문제
https://school.programmers.co.kr/learn/courses/30/lessons/12978
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
배달
N개의 마을로 이루어진 나라가 있습니다. 이 나라의 각 마을에는 1부터 N까지의 번호가 각각 하나씩 부여되어 있습니다. 각 마을은 양방향으로 통행할 수 있는 도로로 연결되어 있는데, 서로 다른 마을 간에 이동할 때는 이 도로를 지나야 합니다. 도로를 지날 때 걸리는 시간은 도로별로 다릅니다. 현재 1번 마을에 있는 음식점에서 각 마을로 음식 배달을 하려고 합니다. 각 마을로부터 음식 주문을 받으려고 하는데, N개의 마을 중에서 K 시간 이하로 배달이 가능한 마을에서만 주문을 받으려고 합니다. 다음은 N = 5, K = 3인 경우의 예시입니다.
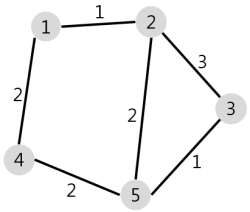
위 그림에서 1번 마을에 있는 음식점은 [1, 2, 4, 5] 번 마을까지는 3 이하의 시간에 배달할 수 있습니다. 그러나 3번 마을까지는 3시간 이내로 배달할 수 있는 경로가 없으므로 3번 마을에서는 주문을 받지 않습니다. 따라서 1번 마을에 있는 음식점이 배달 주문을 받을 수 있는 마을은 4개가 됩니다.
마을의 개수 N, 각 마을을 연결하는 도로의 정보 road, 음식 배달이 가능한 시간 K가 매개변수로 주어질 때, 음식 주문을 받을 수 있는 마을의 개수를 return 하도록 solution 함수를 완성해주세요.
- 마을의 개수 N은 1 이상 50 이하의 자연수입니다.
- road의 길이(도로 정보의 개수)는 1 이상 2,000 이하입니다.
- road의 각 원소는 마을을 연결하고 있는 각 도로의 정보를 나타냅니다.
- road는 길이가 3인 배열이며, 순서대로 (a, b, c)를 나타냅니다.
- a, b(1 ≤ a, b ≤ N, a != b)는 도로가 연결하는 두 마을의 번호이며, c(1 ≤ c ≤ 10,000, c는 자연수)는 도로를 지나는데 걸리는 시간입니다.
- 두 마을 a, b를 연결하는 도로는 여러 개가 있을 수 있습니다.
- 한 도로의 정보가 여러 번 중복해서 주어지지 않습니다.
- K는 음식 배달이 가능한 시간을 나타내며, 1 이상 500,000 이하입니다.
- 임의의 두 마을간에 항상 이동 가능한 경로가 존재합니다.
- 1번 마을에 있는 음식점이 K 이하의 시간에 배달이 가능한 마을의 개수를 return 하면 됩니다.
입출력 예NroadKresult
| 5 | [[1,2,1],[2,3,3],[5,2,2],[1,4,2],[5,3,1],[5,4,2]] | 3 | 4 |
| 6 | [[1,2,1],[1,3,2],[2,3,2],[3,4,3],[3,5,2],[3,5,3],[5,6,1]] | 4 | 4 |
입출력 예 #1
문제의 예시와 같습니다.
입출력 예 #2
주어진 마을과 도로의 모양은 아래 그림과 같습니다.

1번 마을에서 배달에 4시간 이하가 걸리는 마을은 [1, 2, 3, 5] 4개이므로 4를 return 합니다.
function solution(N, road, K) {
var arr=Array.from({length:N+1}, ()=>Array(0).fill());
road.forEach((x,i)=>{{
var [sT,eD,Len] = x;
arr[sT].push({to:eD,dist:Len});
arr[eD].push({to:sT,dist:Len});
//반대로 오는 상황도 sT랑 eD바꾸는 방법을 쓰는게아니고
//반대의 상황도 같이 배열에 넣어야한다
}})
console.log(arr)
const dist = Array(N+1).fill(Infinity);
const queue=[{to:1,dist:0}];
dist[1]=0;
while(queue.length){
const { to } = queue.pop();
arr[to].forEach((x)=>{
const acc=dist[to]+x.dist;
if(dist[x.to]>acc){
dist[x.to]=acc
queue.push(x)
}
})
}
var ans=dist.filter(x=>x<=K)
return ans.length;
}
출처
https://blog.naver.com/ndb796/221234424646
23. 다익스트라(Dijkstra) 알고리즘
다익스트라(Dijkstra) 알고리즘은 다이나믹 프로그래밍을 활용한 대표적인 최단 경로(Shortest P...
blog.naver.com
https://han-joon-hyeok.github.io/posts/dijkstra-algorithm/
다익스트라 알고리즘 개념 정리 및 구현 (JavaScript)
다익스트라(Dijkstra) 알고리즘
han-joon-hyeok.github.io
'알고리즘' 카테고리의 다른 글
| 위상 정렬 (0) | 2023.06.03 |
|---|---|
| 플로이드 와샬(Floyd warshall)알고리즘 (0) | 2023.06.02 |
| 다이나믹 프로그래밍 (Dynamic Programming) - 타일링문제 2 (0) | 2023.06.01 |
| 다이나믹 프로그래밍(Dynamic Programming) - 타일링 문제 (0) | 2023.05.31 |
| 다이나믹 프로그래밍(Dynamic Programming) - 메모제이션 (0) | 2023.05.31 |